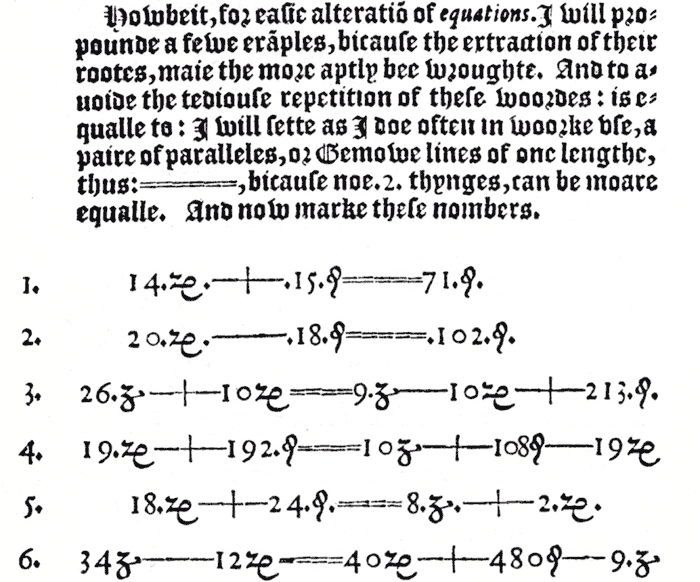the look of math
by mjt
Edited by MJT and Patrick Mahon. First published as a Master of Fine Arts degree program thesis, at and by the University of Western Ontario, in 2011.
Examples
of Ethnomathematical Visuality
Notes of Interest, Elaboration, and Reference
1. Morphism. Steven Dale Cutkosky. Toroidalization of Dominant Morphisms of 3-folds, Issue 890 (Providence: AMS Bookstore, 2007), 6.
2. Illustration of a mathematical limit on the Cartesian coordinate plane. As the curve of the graph continues to the right, it draws closer and closer to the x-axis but never reaches it.
3. This image of the first equation was scanned from a copy of the 1557 textbook by Robert Recorde entitled The Whetstone of Witte. The original publication information (London, 1557) is in my bibliographic entry at the end of this thesis -- what follows refers to the reprint. Robert Recorde. The Whetstone of Witte (Amsterdam: Da Capo Press, 1969). Pages are not numbered.
4. Dieter Roth, Schriftbild (Farbdrucke Von R5-17), 1983/84. One of four. Image reproduced from: Sammlung Maria, Walter Schnepel. Fluxus und Freunde (Weserburg: Neues Museum, 2002), 127.
5. Bill Ralph, Series of 9 on Metallic Photopaper, 19 " x 30", realized digital image. http://billralph.com/PortfolioPages/P057.html, accessed June 23rd, 2011
6. Algebraic statement. This mathematical statement refers to the number of points on an algebraic curve. F. C. Holroyd, R. J. Wilson. Geometrical Combinatorics (London: Pitman Publishing, 1984), 47.
7. MJT, Algebraic Ring, 2010. Marker, ballpoint pen, colored pencil, graphite pencil on 20″ x 30″ rag paper.
8. This triangle is being prepared for folding into a polyhedron. Jin Akiyama, Edy Tri Baskoro, Mikio Kani (Eds.). Combinatorial Geometry and Graph Theory (Berlin: Springer, 2005), 40.
9. MJT, Differential Geometry, 2010. Marker, ballpoint pen, colored pencil, graphite pencil on 20″ x 30″ rag paper.
10. "The lower decker set of the 2-twist spun trefoil." A trefoil is, along with being a variety of Girl Scout Cookie, an object used in topology. This diagram was described to me by an expert as being "a tube wrapped around a knot." David E Radford, Fernando José Oliveira Souza, David N. Yetter. Diagrammatic Morphisms and Applications (Providence: AMS Bookstore, 2003).
11. MJT, Waterslide, 2010. Marker, ballpoint pen, colored pencil, graphite pencil on 20″ x 30″ rag paper.
12. Calculations for wall hangings. In order to evenly hang the drawings detailed in this thesis on my studio wall, I needed to do some calculations.
13. MJT, The Power Rule, 2010. Marker, ballpoint pen, colored pencil, graphite pencil on 20″ x 30″ rag paper.
14. Guitar tuning chart for Three Compositions, the Pitches of the First Being Derived From Familiar Mathematical Constants, the Pitches of theSecond Being Derived From the Harmonic Series, and the Pitches of the Third Being Derived From Sequential Quarter Tones. MJT, 2011. Sound installation.
15. Still (00:00:21) from Trefoil. MJT, 2011. Soundtracked digital animation. A deformed trefoil throbs with the beating of its own heart while algebra floats up into it. Sound is pulsating and low-pitched.
16. Still (00:01:43) from Trefoil. MJT, 2011. Soundtracked digital animation. Tentacles made of algebra catch stylized flies, while we hear a buzzing, feedback-generated music.
“Chess players are madmen of a certain quality; the way the artist is supposed to be, and isn’t, in general.” – Marcel Duchamp
Duchamp [1] (1887 – 1968) was perhaps the only historically important artist concerned with math [2] , in and of itself. Many artists used math as a tool or reference to help develop their works, but Duchamp was quite unique in that he looked directly at its nature and structure, and made it the subject of some of his creative explorations. His career as an artist ended in 1918 [3] , when he moved from New York to Buenos Aires and started playing chess, attaining mastery of the game and continuing with it until his death [4] .
The quote at the top of the page is taken from an interview given by journalist and art critic Pierre Cabanne [5] , published in 1967, one year before Duchamp’s death. In the interview, Cabanne asks Duchamp about chess, and if playing chess was a more satisfying form of personal expression than art; Duchamp answers, “Yes, perhaps.” Earlier in his life, though long after he had replaced art with chess (and in fact after he had realized that his talents at chess were probably not going to develop any further), Duchamp said, “I am still a victim of chess. It has all the beauty of art - and much more. It cannot be commercialized. Chess is much purer than art in its social position.” When Duchamp gave his quotable response about art, madmen, and chess, he inferred that all of the qualities he felt were missing from art and the art world were present in chess. Chess, for Duchamp, had a purity, passion, and incorruptibility that made it an attractive and worthwhile pursuit, one that stood in contrast to the environment with which Duchamp had become dissatisfied.
Moving from chess to math is easy. Like math, chess is concerned with logical processes and structures that are demonstrated and displayed with an inherent visuality [6] ; just as the living logic of a chess game is communicated to us with a particular layout of pieces on the board, the living logic of mathematics is communicated to us with Greek, Arabic, and Roman symbols. Qualities of chess that appealed to Duchamp – purity, passion, resistance to commercialization – are found in pure mathematics. Although my research is not about pure mathematics per se, it is about a ghost of pure mathematics, mathematics-under-glass, or a mathematical Shroud of Turin [7] . Similarly to the way Duchamp saw chess as a way to rejuvenate creative practice, part of my hypothesis is that math, and more specifically the visual culture of math, contains unrealized and revitalizing potential for art. Preceding that assertion is the other part of my hypothesis: that math exists in a two-part structure (visuality and internalities), which can be separated, like blood or cream.
The look of math – its symbols and diagrams – is “significant in its form” [8] as an archive of cultural production. This look of math, or visuality of math, can function as a source of artistic material, or can be regarded as artistic material in and of itself, apart from the logical internalities of the mathematics with which it engages. This line (between math regarded as artistic material in and of itself and art based on the logical internalities of mathematics) needs to be drawn because there is a well-established tradition of art generated from mathematics; for example, the drawings of M. C. Escher [9] , and various sorts of formalist and logical, pattern-based works that use math in the creation of those forms, including African fractals and contemporary computer-generated artwork [10] .
The focus of my study does not relate to these latter examples, on what is usually thought of as “mathematics in art,” but rather focuses on something like mathematical residue – the symbology that would remain on a paper or blackboard if the internal mathematical logic could be taken away. This external or superficial beauty enjoys a complex and peripheral relationship with what mathematicians call “mathematical beauty.” It is notable that classically-termed “mathematical beauty” may actually be a combination of visuality and something like symmetry, completion, logical puzzle-solving – the meshing of mathematical internalities, or a “light bulb flash of understanding.” [11] As I detail later on, it is especially noteworthy that a great many – perhaps even a majority – of examples of “mathematical beauty” presented to a lay audience are presented only when accompanied with some compelling visualization of the mathematics at hand. The reason for this might be that writers and publishers do not trust their readers to associate “the beautiful” with logical math statements, and think those readers need to be helped along into an aesthetic mindset with a “pretty picture.” It might also be that mathematicians and math writers themselves have misappropriated the word “beauty” and are using it incorrectly or too loosely. Mathematical beauty, in spite of its textbook definition, often seems dependent on visual aesthetics, at least as it is usually demonstrated.
My explorations in this paper and in my studio research are about math as art, as opposed to math in art. I consider the visuality of mathematics – the way mathematics looks, as opposed to how it is. It is this superficiality with which I am concerned in terms of my studio work and my academic research. That is not to say “superficiality” in the sense of being shallow or trite, but regarding what the term denotes: concern with surface meaning.
This is a Saussurean project in that it is concerned with a two-part structure of some superficial indicative representative (sign), and some “deeper,” more substantial object to which the sign refers. With this in mind, it would be helpful to go into a small amount of detail about Ferdinand de Saussure’s semiotics and how his posited object-archetypes or containers relate and correspond to the objects of (and objects in) mathematics, ethnomathematics, and the look of math, and the way I am attempting to use the objects in this intellectual undertaking.
Saussure, in his influential and seminal work Course in General Linguistics [12] , mapped out in some detail (and from a particular philosophical perspective) the way visual, auditory, or other symbols work to represent objects in human consciousness, communication, and information retrieval. Saussure saw semiotics as a dyadic, or two-part structure: a given sign is split into a signifier (the form the sign takes), and the signified (the concept or cognitive structure the sign takes in the mind as it is mapped to object, or referent). For example, the ink or pencil mark “2” on a page or chalkboard would constitute the signifier. Then, under normal circumstances and use, the subsequent cognitive task would be to map this particular visual shape, this recognizable and categorizable image, to a mental structure of “2,” which is ontologically similar to an ultimate referent-object of “math.” In fact, in the case of math or other abstract objects (justice, God, love, etc), it becomes difficult to parse a difference between the mental object “signified” and some external object “referent.” So, in these cases it can be useful for me to discard some distinctions, and simplify the Saussurean semiotic structure: all that is needed here, in terms of my project, is a sign or signifier, and then a signified or referent. I am treating “math” as an abstract mental object, and it is not necessary to extract another mental object from it and then apply a label to it; this is redundant.
Mathematics is built from a two-part structure: an internal logical meaning, and those visual symbols that convey this meaning. If internal logical meaning is lifted out from “underneath” the symbols, then the meaning that remains is purely ethnomathematical – concerned with the surrounding (or inherent) culture of math. The visuality of the math that remains, that which creates artistic/aesthetic meaning/presence for an observer, exists because of the cultural content that is left over once the logical internalities of the mathematics are removed. In other words, there is some meaning left there that is of a cultural or ethnological nature, which will of course vary in its particular flavor depending on the observer’s personal, emotional relationship with the mathematical artifacts – which might range anywhere from comfort to fear to disinterest to disgust – or to any number of conceivable human emotions. Mathematics often elicits strong emotions in people, perhaps because of early childhood exposure along with the associated expectations and assertions of society (“You must learn this,” “You must use this,” and perhaps most importantly “You are not smart unless you can do this”). My research is concerned with the potency of this emotional connection with the visual artifacts of math, as well as what that connection’s variable nature can tell us about society and culture, both including and beyond the context of visual art.
For the purposes of my study, I define ethnomathematics as the doing of math, by people; this could be argued to amount to the creation of a visual culture through behavior. In the sections that follow, I will expand on ideas regarding ethnomathematics and representation as they pertain to the phenomenology of visual culture, and then use specific examples from mathematics and art to demonstrate my hypothesis: that in the “pencil-work” of math resides harvestable material for art and visual culture, a resource that has, for the most part, been left unexploited by artists.
Defining “ethnomathematics” would be less problematic if the word did not have a few different meanings. That is to say, the definitional issue is not one generated by complexity or opacity of semantics, but rather by disagreement regarding which relatively straightforward meaning to use. [13] From contemporary usage, three basic definitions describing “ethnomathematics” can be lifted out and categorized: 1) it involves the embedding of math in different social activities, [14] 2) it is any non-Western system of mathematics [15] , and 3) it involves a broader reflection on the sociology of mathematics such that the focus is on a cultural context for mathematics [16] . The first and third definitions are related, although are not precisely the same; the first has a more practical, less theoretical, and somewhat more scientific quality. While I do not want to ignore or pass over the value of this sort of practicality and the kinds of useful examples it demonstrates, my focus in terms of art and culture benefits more from a definition that is not so prone to a reduction to a set of lists or examples. So, it is the third definition on which I will focus, for the purposes of my research into the relationship between “the visual” and mathematics within an anthropological context [17] . The second definition gives rise to political discourse [18] , which is an important consideration, but one that does not directly pertain to visual culture and its relationship with mathematics.
The concept of math being contained within a culture is problematic for many people, possibly because math takes on, for perhaps that same set of “many people,” a universal, almost Platonic [19] set of imagined qualities. The perception of these is, ironically enough, based as much on the cultural perception and social location of mathematics as it is based on any innate or inherent structures. But, in fact, a culture of math must exist; to suppose that it does not exist is to imply that math has nothing to do with human activity. Partly, this resistance to ethnomathematics as a legitimately extant thing has to do with a sort of kulturkampf [20] – a Derridean binary, perhaps – between two real or imagined intellectual camps: we can call one arts, humanities, the textual disciplines, etc., and we can call the other science, technology, engineering, mathematics – sometimes represented by the acronym “STEM” by entities like the National Science Foundation and the United States Department of Labor [21] (and often in the context of certain sociopolitical questions, such as the concern over the relative lack of women and minorities in STEM fields). Basically, the former appears concerned with a right-brained [22] approach to analysis in which meaning is imprecise, while the other takes a left-brained approach, employing precise categorical boundaries. This is a reductionist description of what is, to begin with, a reductionist world-view (and furthermore one that does not necessarily reflect any real political structures of any importance in a contemporary intellectual setting), but it sketches a germane idea.
In light of the foregoing, it is worth recalling that in 1996, Professor Alan Sokal of New York University (in)famously submitted an article to a John’s Hopkins University cultural studies journal. His article asserted that quantum gravity [23] is a social construct, and by strong implication that a scientifically observable, objective reality cannot and does not exist. The journal, “Social Text,” published Sokal’s article, and Sokal shortly thereafter revealed it to be a prank intended to shed light on sloppy intellectualism and scholarship in the humanities. The fallout from the affair included questions on peer review, academic dishonesty, as well as a deeper issue of the humanities’ contemporary hero-worship of the sciences, as a manifestation of the latter’s elevation over the first, socio-politically speaking. The Sokal Hoax, or Sokal Affair [24] , was an iconic and somewhat paparazzi manifestation of the problems whereby the purported two intellectual camps are increasingly, especially in the past 20 years, at odds with one another.
Ethnography, anthropology, sociology – these are all placed in one camp, while math is placed in the other. When the first camp is perceived as encroaching on the second (the root issue that gave the Sokal Affair so much publicity and seeming cultural importance), the conflict between these two elements of the Derridean binary is brought to a head. And true to the form of a Derridean binary, the Sokal Affair demonstrated the “higher” political locus of one element over the other [25] .
Interestingly enough, however, science/math/tech was not always considered culturally “superior” to arts/humanities/text; in Essays on Mysticism, published in 1910, Bertrand Russell mentions that culture studies, history, literature, etc, are taken to be at a higher social location than the technical pursuits of his day. Without delving too deeply into this (which threatens to become a tangential discussion), I would posit that the reason for this shift has mostly to do with World War II, the Cold War (including the Space Race), and the emphasis on industry and production of the military and scientific materials and equipment these events engendered. It is interesting (and comforting to a student of the arts) to know that this world-view was not always in place, and that perhaps university humanities departments were not always as endangered as they are today in a climate of business, militarism, engineering, and the now-familiar chimera of the three.
Returning to the need to locate my definition of ethnomathematics, some of the resistance to the concept comes from the kind of split in intellectual consciousness that I have been discussing, as well as from a haughtiness that stems from the requirements of the military-industrial complex. Arguably, the study of science and technology has been co-opted not only by the “irrational rationality of Capitalism [26] ,” as Michel Foucault put it, but also by the demands of empire.
In science, ideally the process of knowledge acquisition is driven by the scientific method, which is in theory an open process based on experimentation, observation, measurement, and documentation. However, in practice, and especially for lay people, scientific fact is more akin to priestly authority in that it is largely inscrutable, and most lay people do not have the intellectual or research tools to challenge it. Furthermore, in practice, the acceptance of dogma seeps into the professional field as well, often simply for practical reasons; it is impossible to ask “why?” about every conclusion presented in the annals of science – there isn’t time. So, a “life of science” is never going to be wholly about experimentation and discovery; in spite of the existence of rhetoric about the open process of science, some progress within the field will always come out of creed and dogma. In theory, this does not need to remain true; anyone can do their own experimentation and make their own observations to refute mainline scientific consensus, but in practice it is not feasible to do so due to the size of the body of knowledge that is being dealt with and built upon, as well as the complexity of the experimentation required. So, much scientific knowledge comes to scientists in a similar way that creed is passed on by religious authorities and through religious texts.
Mathematics is different than experimental science in this respect. For one thing, one does not need expensive tools to do math. Therefore some potential exists for the lay individual to challenge a public and consensus-based doctrine of “mathematical truth,” something which happens not-infrequently; mathematics has a long tradition of a sort of “amateurism” where people with little exposure to a containing culture, or who are not institutionalized or affiliated, make significant contributions to the field, in the manner of Einstein [27] or Perelman [28] .
Math is called “The Queen of Sciences,” because it is the language with which the experimental sciences operate in their ongoing tasks of observation, measurement, and comparison. These tasks require precision, exactitude, and repeatability, which are abilities mathematics can lend them. But “The Queen of Sciences” is a misleading label, because mathematics is different from experimental science in important ways: 1) it constitutes a creative process, 2) it is less dependent on dogmatic authority, and (most central to my scholarship) 3) mathematics is different from experimental science in that it is inherently visual – a record of the cultural act of doing math is produced every time these tools are used. From that, and apart from the internal logic of math that is responsible for its use in science and engineering, comes “the look of math.”
Simply stated and from my perspective, ethnomathematics is the human act of doing math, as well as all the patterns, behavior, and visuality that result from it, which – depending on your philosophical position vis-ą-vis Platonism and the Realm of Ideas as it relates to mathematics – might or might not be a different thing than mathematics itself. So, the problematic of defining ethnomath goes deeper than the aforementioned right-brain vs. left-brain intellectual kulturkampf – indeed, it is a problem that harkens to one of the oldest discourses in the history of philosophy: realism (math as discoverable object) vs. anti-realism (math as created object).
Along with “doing math,” ethnomath comprises “looking at math.” Any time a human does something, that human is engaging in culture, and is in fact creating culture. Culture can be seen as the sum total of human behavior, although that seems to bring the discussion into the domain of psychology. To expand on this definition, one might imagine patterns in human activity, such that they can be repeated. Certainly, even if one were a strict Platonist-bordering-on-Pythagorean who believes math to be something that has a life of its own, that exists totally apart from human thought, behavior, and culture, such a fundamentalist thinker would still have to admit that math is something that people do.
To prove this, write down a problem: “4x + 4 = 2, solve for x”, then solve it algebraically as you were probably taught to do at 12 or 13 years old. That process of solution seeking involves a human being doing math, and is therefore ethnomathematical in nature. In fact, to take our example of that simple algebraic equation further, we can imagine a class of 13 year olds all doing the same problem, in a classroom, with all of its conventions and codes of certainly no one in a right and reflective mind would argue that the same logical concepts of algebraic substitution could not be accomplished with different symbols.
To answer the question “What differentiates ethnomathematics from mathematics?”, we have to assume one of two philosophical positions, and then give one of two possible answers. If we are mathematical anti-realists [29] , also referred to as mathematical anti-Platonists – that is to say we believe math is nothing apart from that which is created by human beings – then our answer verges on “Nothing; there is no difference,” since math’s inability to exist apart from human activity turns ethnomathematics into a sort of absolute unto itself. However, if we are mathematical realists or a mathematical Platonists, such that we believe math is a universal thing that exists whether humans are involved in it or not, then the answer is “There is a difference – math per se is not the same thing as doing math.” In this case, the object of “math,” as it is Platonically imagined, does not necessarily have anything to do with the human act of doing math, which in this case is taken to be something like discovery or even spiritual revelation of some sort of universal or divine truth.
And “divine truth” is what math was taken to be in the time of Pythagoras and in the time of Plato [30] , with Pythagoras going so far as to implement a religious cult around mathematical and especially geometric absolutes. For Pythagoras, math was divine; it was the language of the Gods. And Pythagoras influenced Plato, notably in his ideas that mathematics can form the basis of a universal truth or ideal [31] .
Different sorts of contemporary mathematicians might answer the question of whether or not math is a Platonic ideal differently. First, consider mathematical physics, which is concerned with quantum and particle behavior illustrated in theoretical models. [32] For mathematicians in this field, math is being used to describe particularities within our own universe – physical realities that do not necessarily have counterparts in all of existence; a mathematical physicist might thereby come to see math as an anti-realist construct, or something that is wholly human-created. However, in a very abstracted field like category theory [33] , which is based on the articulating or demonstrating of the relationships between mathematical objects without necessarily going into any detail about the properties of the objects themselves, the math has no reference point to a physics or set of natural laws that is uncertain to exist in any “reality;” it is therefore multi-universally true that any number of extra-dimensional civilizations would be likely to invent the same “category theory.” So, to a category theorist, math might seem more like a Platonic ideal: a universal that supersedes human creativity, or even a discoverable object.
The question of whether math is created or math is discovered is philosophical, and open-ended. Although mathematical realism and ethnomathematics are connected, they do not enjoy a logical relationship such that some particular position (notably, that of the mathematical anti-realist who might be inclined to assert that ethnomathematics and mathematics are not significantly different things) will cancel out the existence of ethnomath. Perhaps our discussion regarding mathematical realism may broaden or narrow the scope of ethnomath or make it indistinguishable from math per se (that is to say, innate logical structures), but such conjecture is still not able to extinguish ethnomathematics as a term altogether for one simple reason: people do math, read math, and maintain a working relationship with math within which behavioral norms are established. A culture of math is a necessary thing, its existence just as tautological as the existence of a culture of religion. As an anthropologist might study the culture of some facet of a particular society – marriage customs, sexual morality, funerary practice, etc. – so he or she might study the culture of mathematics.
“Pure mathematics” is a particular facet of that refers to math that is pursued and done for its own sake, without any desired or foreseen application [34] . I bring up this distinction for two reasons. Firstly, as I pointed out above, it should be noted that some branches of mathematics lend themselves to an anti-realist world view, while others lend themselves to a realist world view, depending on whether their work appears to be related to physical or natural phenomena, or if the mathematical work is abstract enough to constitute sufficiently generalized categories and objects to sever any connection which that mathematics might have to the natural world. Secondly, I bring it up because “pure mathematics,” and the distinction between “applied math” and “pure math” is an ethnomathematical distinction [35] . The philosopher and mathematician Bertrand Russel, in his Mysticism and Logic, tells us that pure mathematics was invented or discovered by Boole in 1854, and “consists entirely of assertions to the effect that, if such and such a proposition is true of anything, then such and such another proposition is true of that thing.” In general words, pure mathematics is a philosophical system based around formal logic, that stands in contrast to the real-world problem-solving tools of applied math.
The distinction between math-in-art and math-as-art is important. Math-in-art, as I have stated, is art where math is used to generate the artwork, where the logic and operation of mathematics is seen as functioning in a “classically mathematical” way. Good examples are the work of M. C. Escher in which geometric forms are precisely interlaid, and contemporary computer art that makes use of the computational ability of a microprocessor to calculate visual geometric relationships that would be challenging or impossible to do by hand.
Diagrammatic Morphisms [36] , a kind of string diagram used in contemporary topology (and which I use in my own artwork), are a borderline-case, although less of one than they might appear to be, once one understands the nature of morphisms. This begins to move uncomfortably into overly conceptual waters, where form starts to depend on its cultural context, but I think a solid analysis of this area is still possible. Diagrammatic morphisms appear to be art; that is to say, they are pictorial, and made of shapes and lines. They do not appear to be symbols, something that would fit, in a less alarm-raising way, into the paradigm of math-as-art. Instead, they appear to be math-in-art – some shapes that are ultimately generated by math. Of course, one might argue that the way they appear, especially to a layman, is secondary to their intrinsic nature. One suspects that something so formal, in mathematics, must “have something to it” – that it could be a manifestation of “math-in-art.” In fact, this is not the case, and diagrammatic morphisms are best described as symbols or signifiers. If one were to derive “math-in-art” from them, that art might look something like a deformed rubber sheet (a familiar metaphor to scholars of topology who endeavor to explain their field to lay audiences). But in fact these diagrammatic morphisms are something more akin to algebra – a way of representing a logical internality that eventually manifests or generates, at least in theory, something overtly visual. This is to say diagrammatic morphisms are not the “end product.” They are not “math-in-art,” but are a rather interesting example of “math-as-art,” because they look like they might be “math-in-art.”
I say these waters might be overly conceptual because if a given piece of math has visual properties, we need to ask whether or not it could then be called visual ethnomath. Indeed, morphisms are a border case, because of the potential for a superficial, lay interpretation of them as some kind of art that has been generated by math. Furthermore, this “lay superficiality” is precisely what I am concerned with, culturally, artistically, and from a research standpoint.
The most obvious examples of “math-in-art” all come from geometry; the challenge comes in finding an example that does not infer that the visuality of math is necessarily tied to its geometric offspring. Consider category theory, that very abstract branch of modern math where objects are posited, and structures are built from their relationships, without necessarily elaborating on the properties of those objects, per se. [37] What is “generated” from category theory? Most obviously, morphisms (and not necessarily diagrammatic morphisms, which help bridge the gap between topology and category theory [38] ).
As seen at the bottom of the previous page, morphisms (basically, a mapping between two mathematical structures [39] ) look geometric. And since they are associated with math, the general assumption could be that their pictures must have been generated by math, as a right triangle is generated by the Pythagorean Theorem. And, in a sense, they have been generated by mathematics – they are the structure resulting from pre-existing relationships and objects. A morphism amounts to b derived from a, which is perhaps the only important thing we need to remember in terms of morphisms being an example of math-in-art (as well as, clearly, math-as-art). Perhaps we can illustrate the relationship of math-as-art and math-in-art by imagining a Venn diagram: all math-in-art is math-as-art, but math-as-art is not necessarily math-in-art. Regardless of this, and regardless of those aforementioned fuzzy gray areas, the distinction remains: math can generate form, and math can be form. As stated previously, I am concerned with the latter.
Formal beauty, ethnomathematical beauty, and mathematical beauty appear to have some sort of relationship. When definitions of mathematical beauty are given, often nothing related to visuality is expressed, but in order to communicate the notion of beauty there might be a diagram or picture in which a sort of elegance, symmetry, or order is visually present [40] [41] [42] . It is as if these definitions are expected to be insufficient, and it is therefore felt that they need to be supplemented with something more conventionally associated with “beauty.” This is understandable, considering that the word beauty has historically been associated with visuality, or more specifically, with the phenomenal.
Mathematicians and adherents of math may be semantically altering, or even misusing, the term “beauty” when they talk of “mathematical beauty.” With qualities like succinctness, surprisingness, elegance, insightfulness, originality, and the ability of a proof to be easily-generalized being said to indicate beauty [43] , it becomes arguable that any field in which there is some task to be accomplished, could refer to “x beauty” in terms of a method if that method tended to accomplish that given task, where “x” is an adjective that describes the field of endeavor. For example, perhaps “medical beauty” could refer to stitching up a cut optimally, such that it heals well, and perhaps “clerical beauty” could refer to alphabetizing forms quickly and expediently. Using the term “beauty” to refer to what is essentially mathematical competence seems to elevate the discipline, socially and politically, establishing the phenomenon responsible for much of the leftover visual culture of mathematics, once the mathematical “guts” are cleaned away.
Euler’s Identity is probably the most frequently-given example of mathematical beauty [44] , and is familiar to some laypeople (such as myself – I heard about it in a first-term calculus class in 1999):
epi + 1 = 0
In Euler’s Identity, we have the five most important numbers in mathematics, along with the three most important operations: e, i, pi, 1, and 0, as well as exponentiation, multiplication, and addition. This is a relevant example for an art-related discussion because, visually, it is not particularly interesting (or beautiful); the “beauty” inherent in this simple equation comes from its logical content, so there is no confusing mathematical beauty and formal beauty here. In this way, the mathematical beauty at hand is of a pure sort, uncontaminated by visuality or perhaps even by ethnomathematical considerations. Rather, this simple equation just is, as it is. Usually, examples of mathematical beauty seem to somehow “cheat” and give snippets of visuality to help the beauty along, but in this case the “beauty” is entirely logical. And by “beauty,” in this case, something like great power expressed in simplicity is being advanced through the use of the word. The beautiful thing here amounts to a question: how, and why, in our universe, do the five most important numbers in mathematics fit together and relate to one another as simply as they possibly could?
To say that I have some experience with math is also to say that I have some experience with the look of math. My experiences were similar to those of many others: I was required to take math classes in primary and secondary school, mostly disliked them, and did a mediocre job at them. In 1997, I experienced a traumatic brain injury that changed that. After being hit by a car and then convalescing for several months in and out of the hospital, math was still not easy for me, but it had become fascinating, meaningful, and exciting. For many years I re-told a mythology to explain my newfound love of math: the “shear-injury” [45] had damaged my right temporal lobe, and with my poetic powers of apprehension compromised I [46] turned more to my left-brain to make sense of reality. This more logical approach meshed well with the intricacies of introductory college mathematics I encountered in a required class I took in the late 1990’s, and my success there inspired me to pursue additional study. In spite of the appealing romance of this story, my success in math could have mostly been the result of having a good pre-calculus teacher, or of being mature enough at that point to make a serious go of school – or x, or y, or z. But the mythology of my left-brain kicking in to help out my damaged right-brain became important to me as I re-told it again and again, even as brain science research stated that the division of cognitive labor might not be so clear-cut. [47]
I should add here that I thought at that time that the joy I experienced in doing math had some kind of spiritual significance. And while perhaps the fact that it felt significant made it significant, I am now more inclined to think, perhaps cynically, that my experience was not much different from the satisfaction one gets when solving a crossword puzzle. Here was something that worked out: a right answer, some bit of beautiful and “intricate simplicity,” in the face of a largely uncontrollable and confusing reality of existence. The pleasure of “getting it right” had little to do with my teacher’s assurance that I was doing the right thing, but what mattered was the fact that I could match solutions with what was perhaps a universal template; there is a right answer to math problems, which constitutes a satisfaction and fulfillment that a student of the humanities might never experience. This could have accounted for the feeling of Pythagorean mysticism I was experiencing; I was in my early 20’s then, and I think at a good place, emotionally and mentally, for learning and doing math.
I remember one day in pre-calculus class particularly well: something about trigonometry was being explained, and tears came to my eyes because I “got it” so thoroughly; this symbolic and logical system made so much sense, and it all seemed “perfect.” Especially in light of that experience, I can now see why Pythagoras equated the sense of perfection sometimes associated with math with the tautological perfection of God [48] . But was this a Jamesian mystical experience [49] ? Certainly it was an individual experience, one centered on the phenomenological apprehension of a perceived nature of reality. Perhaps all math – the doing of all math – is inherently (at least potentially) a mystical experience, because it can have a sense of “revelation” attached. And perhaps the sense of revelation – getting a “right answer,” not according to a teacher’s edition textbook, but to a universal template of how the universe works – indicated that I was having one of only a few spiritual or mystical experiences in my life.
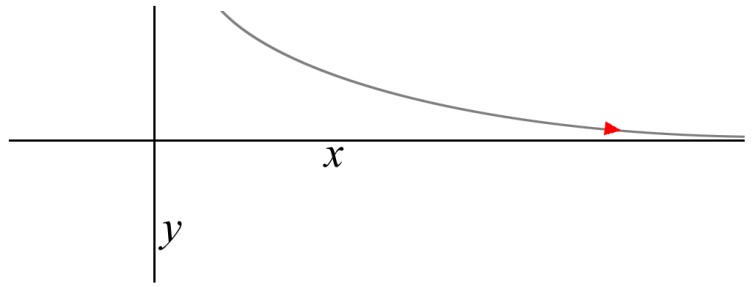
As I advanced to calculus, the concept of limits again harkened to something universal and meaningful, just as trigonometry had a few months earlier (notably, the function of both limits and trigonometry are both commonly illustrated graphically). A limit involves the concept of a thing approaching another thing, and continuing to approach it forever, without necessarily ever reaching it. This concept is well-illustrated by a parable called “Xeno’s Paradox.” Imagine that an archer shoots an arrow at a target 10 meters away; in order to travel to the target, the arrow must first travel half the distance (5 meters). Then, in order to travel the remaining 5 meters, the arrow must travel half of that distance (2.5 meters). And again, and again, the arrow must travel smaller and smaller distances to traverse the now seemingly infinite expanse of 10 meters. It seems, if approached this way, that Xeno has demonstrated that movement is impossible. Of course, it is not, and arrows reach their targets when they are shot at them. But Xeno’s paradox works to visually demonstrate the nature of the limit, which operates similarly to Xeno’s arrow. A good way to illustrate a limit is with a coordinate plane:
As you can see, as the curve continues to the right, it never reaches the X-axis, but only becomes closer and closer to it as it approaches a distance infinitely far from the Y-axis. Incidentally, the limit of this function (represented by the curved line) would be said to be 0, because that is the number, as it is represented graphically by the x axis, to which the function draws infinitely close but never reaches. This rigorous dealing with infinity also contributes to what might be construed as the overall spiritual or mystical feeling of calculus.
Is math, or can math, be more than the marks on paper that we write down and see? Is it really possible to separate out the working guts of math – the logical internalities, as I put it earlier, from the pure visual representation of math? If the math we see on the paper is the signifier, then what is the referent? These questions point to an over-arching issue: that of “deep” vs. “shallow” understanding of mathematics.
The “shallow” approach is the easier to explain, especially with the help of examples, the first of which I will take from pre-calculus algebra. When dealing with negative exponents, one has another notation option: to convert them to reciprocal fractions with positive exponents, which are sometimes easier to deal with. In this way, x-4 becomes 1/x4. Without understanding why this “trick” works, it is very easy – trivial, one could say [51] – to memorize that whenever you see something of the form x-n, you can convert it to 1/xn, and thereby get the right answer. This is an example of the “if you see this, do that” mentality, and it is prevalent in students’ approaches, probably on up to analysis [52] . At its essence, it is an approach based on memorizing tricks and patterns without really understanding the inner mechanics of how a given theorem or formula of mathematics works.
And this approach – this “stupid human trick” method of doing math – becomes more and more ingrained, and in fact becomes more and more necessary, as a student advances to calculus and beyond, where a myriad of tricks and shortcuts have been developed for differentiating (also known as “taking the derivative of”) functions of various types. In every math text I have seen, the reason a given trick works is demonstrated using the algebraic definition of the derivative, as it was developed by Newton and Leibniz, as a sort of “proof” (although not in the strict mathematical sense), and then the simple mechanical gesture of manipulating the math symbols in the correct way to get the right answer is demonstrated.
A good example of this comes from differentiating a function of the type f(x) = xc (such as f(x) = x3). The example function’s derivative, or f′(x), is 2x2. All I had to do in this case was take that “3,” put it in front, then subtract 1 from the exponent, so as to turn 3 into 2. This is mindlessly easy – far easier than doing the multiplication and long division one learns in elementary school – and the process (using “the power rule”) works to take the derivative of a function of type xc every time (where x is the algebraic variable and where c is some constant).
The reason the power rule works has to do with the algebraic definition of the derivative (itself often considered to be a thing of mathematical beauty), and measuring variable change. This can be illustrated algebraically, and a simple function like f(x) = x3 can be differentiated algebraically by plugging it into the definition of the derivative. But this is, relatively speaking, a time-consuming and tedious process, and there is simply no need to do it other than for explanatory purposes – to try and impart a “deeper understanding” of math. For people like engineers and physicists, who need to take derivatives in order to solve problems in their fields, there is no need to learn about the algebraic definition of the derivative and how to differentiate functions “the long way;” all they need to learn is the aforementioned trick, and a whole battery of tricks like them: “The Product Rule.” “The Reciprocal Rule.” “The Quotient Rule.” “The Chain Rule.” Etc. [53]
Math is thereby reduced to something like a Sudoku puzzle or Rubik’s Cube; certain configurations of symbols that appear on a paper are manipulated in certain memorized ways, which then yield the right answer. For people who use math in some professional capacity (such as engineers and experimental physicists), this is all they ever need to know. They do not even really have to learn about the definition of the derivative that one first time, when they might be forced to plug a function into it to differentiate “the long way” for the purpose of understanding how the nuts and bolts of math work, before they quickly fall back on a series of memorized symbolic manipulations.
If these symbols are being manipulated and manipulated correctly, and it can be determined that some deeper understanding is thereby being ignored, then what is this “ignored thing,” and what are its parameters? What constitutes a “deep understanding” of math? It is difficult to quantify, most obviously because it is subjective – if someone were to assert that he or she had a “deep understanding” of math, then could this self-report be successfully debated with the response “No, you don’t”? In spite of this difficulty, I see three ways to investigate a definition of “deep understanding.”
Firstly, the method for achieving mathematical depth might be as I infer above: by understanding and working with the proof and derivations of every formula one uses to solve problems. The pitfall here is that in working with these proofs and derivations it is necessary to perform the same sorts of symbolic manipulations one started off doing when solving the original problem, and so in a sense one is no further along in achieving depth of mastery. In other words, one can never escape “doing math” – it will always consist of symbolic manipulation, regardless of the fact that a particular sequence of manipulations might represent a meaningful derivation of some used formula.
A second possible definition could employ similar terminology to that used in defining or expounding upon mathematical beauty – especially in the generalizability of some particular bit of math: if enough rote calculations or symbolic manipulations are performed, then a larger picture might start to become evident from the continuity of mathematical truth that reveals itself. For example, if a student were to take courses in single and multi-variable calculus, linear algebra, differential equations, and finally real and complex analysis, then maybe after the solution of every problem in every associated textbook some deep understanding of math might seep in, in the midst of a cognitive state similar to the later stages of language acquisition.
Finally, can a deep understanding simply be defined in the negative, as anything a shallow understanding is not? It is straightforward to define a shallow understanding of math as symbolic manipulation, performed as though the mathematician were nothing more than a computer. With this in mind, perhaps we can surmise that emotional creative content – that which our hypothetical, robotic, shallow mathematician does not possess – amounts to that “deeper understanding” of math. This creative input and approach amounts to math-as-art, or more precisely, math as an art.
The difficulty we encounter when trying to establish some parameters for the mathematical referent – that part of the two-part math structure that is not merely the symbols and their visuality – again speaks to an inherent ineffability and mysticism within the discipline of math, similar in that sense to Platonic ideals of math “existing” somehow beyond human exercise, and also similar in that sense to the notion of mathematical beauty. But most importantly, in terms of my discussion, it is these symbols and their manipulation, apart from any sort of mathematical depth, whose visual culture is to be exploited. So, when the content is lifted out leaving the superficiality with which I am concerned, it is analogous to the superficial symbolic manipulation of “human-trick math,” which works, but ignores the depth required to explore mathematical beauty.
Examples of Ethnomathematical Visuality
In
this chapter I will present three brief examples in math that illustrate a
relationship between visual culture and mathematics, the first focusing on the
development and history of mathematical notation, and the second and third both
dealing with contemporary mathematics as it relates to my own artwork.
Robert Recorde (1510 – 1558) developed what we know as the modern “equals sign” based on his graphical interpretation of his own phrase: “no two things can be more equal.” It was featured in his 1557 textbook The Whetstone of Witte:
“And to auoide the tediouſe repetition of theſe woordes : is equalle to : I will ſette as I doe often in woorke vſe, a paire of paralleles, or Gemowe lines of one lengthe, thus: =, bicauſe noe .2. thynges, can be moare equalle. ”“And to avoid the tedious repetition of these words: "is equal to", I will set (as I do often in work use) a pair of parallels (or Gemowe lines) of one length (thus =), because no two things can be more equal.”
Recorde’s development of the equals sign, now a ubiquitous part of visual culture, both in mathematics and in a wider semiotic context, was a design decision – a hieroglyphic that Recorde thought captured the notion of quantitative equality. In this way, Recorde’s usage demonstrates a sort of anti-Saussureanism, to perhaps make an extremely simple point sound complicated. Saussure’s idea about signifier and referent was that there is no intrinsic relationship between the sign “cat” – the text on paper or spoken out loud – and the referent cat, the thing that walks around and meows; the relationship is arbitrary and constructed. But, in the case of Recorde’s equals sign, we see that it may be said to inherently resemble equality. In fact, this is why he chose it, although it is not difficult to see that it is not exclusively true that “noe 2 thynges, can be moare equalle” – his equal sign might have been two dots, or two squares.
As an artist and researcher, my focus is “math-as-art,” which implies the usage of the look of math without math’s functionality. This leads directly into questions surrounding mathematical notation, and its development; “the look of math” ultimately amounts to “the way math is written,” and the way these cultural categories that are so familiar to us (such as the equals sign, addition symbol, subtraction symbol, etc) carved out their place within a larger visual culture.
Consider a set of mathematical objects called “diagrammatic morphisms,” which feature prominently in my artwork. They are mathematically significant in that they represent a kind of intersection between topology and category theory, and artistically significant because they are complex line diagrams that are intended as symbols for topological structures – in other words, they are representative math, as opposed to math-generated structures. This might make them “math-as-art,” and not “math-in-art,” except that a dichotomy of the generator and the generated is a causality structure that is easily broken (especially as mathematics become more advanced), and in fact analysis of mathematical forms as either being the result of some kind of calculation or being the calculation themselves is something that is often and largely beyond my ability.
A morphism, as the term is used in mathematics, is a structure of relationships, a precise way of defining how elements in one set map to elements in another set. The complexity of morphisms can become such that representing them diagrammatically, as opposed to algebraically, is the only viable method. In fact, in terms of pure visuality, diagrammatic notation is not limited to morphisms, and a more general term for the sorts of things that look like the sorts of things I like to draw might be “string diagrams.” “Morphism” comes out of category theory (and is in fact at the theoretical center of category theory), and I use the term mostly because the string diagrams I copied happened to be diagrammatic morphisms. However, I think it is important to note that for the purposes of my explorations of the visuality of math, either string diagrams or diagrammatic morphisms would suffice – certainly I would not have been able to tell the difference.
My mathematical abilities are limited; I took one year of calculus, and most of my understanding of it has faded from my memory. And as far as my (art) audience is concerned, it has been my experience that a discourse of calculus, or perhaps any sort of “guts” of math, makes people’s eyes glaze over as they wonder if they are really reading a text rooted in the visual arts. Furthermore, the nature of mathematics is such that one topic leads into the next, without a clear delineation between them (perhaps ironically contrasting with the nature of most mathematical objects themselves [54] ). So, when I find in my research into this rather alien world that the phrase “Diagrammatic Morphism” might not be precisely correct, and that in fact “Penrose Graphical Notation” [55] might be a better way to say it, but then I find that the pictures associated with Penrose graphical notation do not look like the drawings I have done, and that I also need to wrestle with the geometric term “tensor,” I am reminded that I am an artist, and not a mathematician. The best way for a me, a non-mathematician, to go about rigorous scholarship and research into mathematics is to give the titles of some books that I am looking at or have looked at, and perhaps with some help arrive at a generalized understanding of a given field, which leads me into my final “case study” in math: the prose used in advanced mathematical papers.
As a study of math moves to higher scholarly levels, much of the associated text reads like prose. Some of it is highly incomprehensible to a layman, and becomes so specialized and laden with terminology that it can take on a surreal or absurd quality (“A somewhat more promising alternative is to sum over all the diffeomorphism equivalence classes of embedded spin foams. This idea is rather natural […]” [56] ). However, some of the prose is often quite non-technical, and paints things in very broad strokes, using a language couched in metaphors that sound almost literary:
What is truly remarkable about this theorem is that, on the one hand, framed tangles are (relative versions of) central objects in 3- and 4-manifold topology, and on the other, the axioms for a ribbon category flow inexorably from the internal structure of category theory once it is realized that braided mononoidal cateogries are, in some sense, more reasonable objects than symmetrical mononoidal categories. [57]
Regarding the above, my attention is particularly drawn to “the axioms for a ribbon category flow inexorably from the internal structure of category theory,” and the notion of braided mononoidal categories being (in some sense) more “reasonable” objects than symmetrical mononoidal categories. Certainly something “flowing from the internal structure” of a field of math is not a technical description of object behavior – how fast does it flow? How far? And what does it really mean to “flow,” if we presume (hopefully intelligently) that this is a metaphor? And then, we have “reasonable,” even with the added caveat-like phrase of “in some sense.” This example sentence seems, even to a layman like me, a far cry from the precision and discreetness regularly associated with mathematics. It is prose; hand-wavy [58] prose employing imprecise, literary terminology. It surprised me when I first noticed the existence of such language in advanced mathematics papers, and I find its existence relevant to my own research interests, broadly termed as the culture of mathematics, or “ethnomath.”
The sort of “dumbing-down” of concepts, or blunting them into literary forms that we see in these advanced papers on mathematics is a similar process that I am going through when I take algebra, diagrams, or geometry and “dumb them down” into artwork. It is my own impulse to use such pejorative language, and I do so in a similar though harsher way than with my use of the term “superficiality” early on in this paper. So, math is smart and art is dumb? Maybe, depending on the definition of “intelligence.” [59] The fact that the transformation of math into literature or the transformation of math into art lends itself (perhaps only in my writing, but I doubt it) to terms like “dumbing down” or “superficial,” that are in turn sometimes perceived as being indicative of a “lowered state,” might tell us something about that primitive, politically-charged, Derridean binary of right-brained vs. left brained, and arts-humanities vs. STEM (Science Technology Engineering Math). Specifically, it confirms what Derrida tells us: that one of the states of the binary is going to be politically elevated over the other. And, true to form, and as I mentioned earlier, STEM is “higher” (at least in contemporary culture) than the art and humanities. My artwork is in part “about” this phenomenon: that the social location of mathematics is an elevated one for most people, and that transplanting this location into math-as-art does something, I suppose tautologically, to its social location.
The existence of prose like this in math papers as well as the positive reaction I get from people who deal professionally and classically with advanced math when they see my drawings makes me think that this Derridean binary is illegitimate [60] , and that the yearning we see in arts-humanities to co-opt some of the technical rigor, clarity of definition, and non-fuzziness of sci-tech has a converse counterpart: that science needs art, and wants art. The impulse to shy away from algebra and move towards mathematical diagrams that is sometimes necessary in higher mathematics for expediency's sake leads me towards this sort of thinking as well; the adage “a picture is worth a thousand words” seems to apply here, and to the many pages of algebraic topology (or topological algebra) that would be necessary to represent a single, elegant string diagram. This is the visuality of math.
The questions I pose around math-as-art vs. math-in-art, and regarding the possibility of “lifting out” the logical internalities of math to leave behind a relic of visual culture which is then granted new meaning, and concerning the possibility of a relationship between formal and mathematical beauty, are not completely new. Three case studies in the tradition of visual and conceptual art follow, which elaborate on the relationship I am attempting to build between math, culture, and visuality.
As I mentioned in the first paragraph of this paper, Duchamp was probably the only historically important artist to engage with mathematics directly, such that the nature of math was conceptually integrated with the work itself. In his writings, as an example of his “non-retinal art” [61] which sometimes took the form of puzzles or brain-teasers, we find the following: [62]
Calcul par l'absurde mathématique algébrique -
Si A=intention 10.
B=Crainte 5
C=Desir-
on a une premiŹre équation
C=a-b
et une 2 équation
C=A x B
Math ces 2 éq. sont absurdes
C=50 / C = 5 / 2C = 55 / 2=27.5
Si A = 10 / B = 5 / c = 27.5
Si A = a = 9 / B=a/ 3 =3/ C +33/ 2=16.5
Variables are assigned to “intent” (intention), “dread” (crainte) and “desire” (desir), and the interrelationships of these emotional states hinted at with mathematical properties: desire is given to be intention with dread taken away, and in a second analysis desire is intention “multiplied by” dread (the first equation, I think, seems more intuitively correct). Following that is mostly nonsensical algebra. Calcul par l'absurde mathématique algébrique (“Calculation by absurd mathematical algebra”) amounts to a critique of math and logic – obviously math is incapable of elaborating on human emotion, and this shortcoming is illustrated with absurdity. The piece is certainly an example of “math-as-art,” although it is conceptual and not at all concerned with visuality.
Duchamp's conceptualism constituted an originary moment in the history of conceptualism, and as an artist he took such an approach as far as it could be taken; one wonders if his frustration ensuing from this dead-end was what drove him from the art world. But regardless, in order to explore math for math's sake – to explore math-as-art – he delved into the conceptual, and moved away from visuality as a significant aspect of his work. In my explorations, visuality is vitally important – in fact, it is literally all I have once I take away the concept, or logical content, or utility, or machinations of mathematics. I am left with a husk, a shell, which then has the potential to be filled with new meaning.
My second case study has to do with form rather than content. Dieter Roth’s Schriftbild does with text what it is my goal to do with math: it lifts out the internal structure of the referent and ascribes to it a new visuality and cultural meaning. In fact, this specific piece by Roth, translated into English as something like “Writing-Drawing,” was the one of the earliest, if not the earliest, inspirations for the “math-drawings” that I have mention repeatedly in this essay. Roth’s process appears to have been to scribble down love letter after love letter, one on top of another, until the meaning of the text was made all but illegible and had instead formed an image – it had re-contextualized itself from a reliance on codified semiotic meaning and towards a broader visual, formal, adherence to pictorial meaning.
My math drawings look almost nothing like Schriftbild (above) – every line of math in my drawings is legible, and although they are often crowded image-fields, they tend not to be so chaotic. Rather, the point of similarity between Roth’s work and my own work is between Schriftbild and my textual scholarship: regarding math-as-art, and removing logical meaning and transforming visual artifacts of symbols into images. Roth does this by obscuring the text with more and more layers until everything has become illegible, and I do it on the understanding that the vast majority of my audience will be unable to de-code the mathematical forms I use, thereby allowing for their assignment of a new meaning through a new approach to visual culture: an approach generated by a given observer's personal, emotional relationship with these mathematical symbols.
Sometimes, the proverbial 1% of the viewers has the required background in, say, algebraic topology to make some mathematical sense out of my displayed math. This has happened three times at the time of this writing, and in each case the schooled observer responded favorably. The pitfall I would have anticipated when dealing with a “literate” observer might have raised questions surrounding mastery and competency. [63] I might have expected the accusation, “You don’t have the right to be using this math, because you don’t understand it.” In fact that question has been posed, but never by the professionally math-literate; on the contrary, the math-literate seem thrilled that their discipline's inherently visual nature is being treated as something worthy of focus by someone working in the fine arts.
The
important parallel between Roth's Schriftbild and my work is the separation of form from utility; as meaning is taken
away from symbols, they are then infused with new meaning. It is impossible for
a symbol to exist and to be devoid of meaning. For example, in my artwork, if
mathematical logic is taken away from “2x + 4 = 8,” then we are left with
Arabic and Greco-Roman symbols – the mathematical notation of algebra.
This is a more shared meaning than the codified mathematical meaning, simply
because it has a historical and cultural context that is built into it, rather
than having a set of assigned logical properties that are fairly arbitrarily
assigned. There is a reason the “2” looks like a 2, and the “x” looks like an
x: the development of each of these symbols has a history. However, the logical
operation of these symbols is not based on that specific history or culture,
and can be lifted out from, or de-mapped from, the symbology. For instance,
This is the case with Roth's Schriftbild: because the legibility of the love letters has been taken away, we are left with the possibility of some other form of meaning holding sway, one that is not necessarily obvious. Meaning could reside in the subconscious mind [64] , or in the observer's own feelings about art. The difference comes from the fact that in Roth's images, the symbols themselves have been combined and laid one atop the other such that they are actually no longer readable, whereas in my images, the obfuscation of meaning is contextual rather than formalistic. But the central idea of separating inner and outer structure is what makes Schriftbild an important inspiration for my studio work.
Earlier on I gave the work of M.C. Escher and the work of some contemporary computer artists as counter-examples of “math-in-art.” However, there is a fine line here: sometimes when something is “math-in-art” – when a given work has its form generated in part by math – it also ends up being at least in part about math. This leads me to my third and final case study in art.
The contemporary work of Bill Ralph amounts to computer generated images, but inside his concept is also some interest in math for its own sake. The artist says, “What drives [my] process is the extraordinary and often chaotic mathematical behavior of systems built on the iterated function sequence x(n+1)=f(x(n)) where f is a function carefully constructed for its mathematical and artistic interest. [65] ” Bill Ralph’s area of math is algebraic topology, which is perhaps not coincidentally what I find to be the most fruitful area of math from the standpoint of visual culture, and it is this area on which several of my own “math drawings” are based.
I offer Bill Ralph’s work not as a formal example (the look of his artwork is that of contemporary computer-generated images, and is not of particular interest to my research) but because it involves the grey area to which I have referred. In fact, perhaps artists who rely so exclusively on mathematics (or computer programs) in creating their work cannot help but make their work at least partially about these things. Self-reflexivity is a well-traveled conceptual avenue in contemporary art, one that fits in well with the Postmodernist orientation that generates this text, as well as in mathematical constructs like Bill Ralph’s “x(n+1)=f(x(n)).”
Although Bill Ralph is a professional artist whose curriculum vitae documents exhibition, the primary focus of his career is as part of the faculty in the department of mathematics at Brock University in St. Catherine, Ontario, Canada. From this social location we can reliably determine the importance of mathematics in his work – not just as the “engine” behind its formal content, but as a thing for Bill Ralph to focus on in and of itself. Although he does not make any pictures of math in the same way that I do, the implicit math in his images takes on more importance than merely as a tool of production, even if we can only determine this by reading his website, noting his profession, and reading the way he conceptually frames his artwork. In other words, if I were not given some conceptual and textual background for his work, I would assume it to be purely an example of math-in-art. However, since B. Ralph in effect says “I am a math professor, I am interested in math, here is how I derive my images, and here is an example of some of the math I use to derive them,” this proverbial wall-text is now next to all of his creations, and nudges them over toward “math-as-art” and into the paradigm of ethnomathematical visuality.
In my studio research, I am exploring the visuality of math using familiar materials: white 20″ by 30″ Stonehenge rag paper with its iconic rough edges that, at least to me, indicate a sort of archetype of “art supplies.” Process-wise, this project enjoys something of a complex history. The original inspiration came from Dieter Roth’s Schriftbild, which are a series of love letters layered over top of one another, so that they look like a jumbled pile of colorful scribbles. As it happens, my old day planners, which I have saved since around the time I started my flirtation with academic mathematics, contained some forms that were almost identical to Schriftbild. My thought when I recognized this was, “Why not do something similar to Schriftbild, or similar to my day planners, but using math instead of love letters?”
Conceptually, my explorations center on the visuality of mathematics, as it is either organically generated through doing math, or copied from math other people have done. Making this distinction is important, in that the question as to whether a drawing constitutes “real” or “virtual” mathematics (constitutes working math or visual artifacts of math) has implications for not only the art-making process but the result and observation. The first type of drawing involves harvesting a source like a graduate thesis in mathematics for its visual content. The result of this is a sort of sterility and mausoleum sensitivity about the mathematics, which is not necessarily undesirable; having a wax museum of mathematical artifacts is an interesting prospect for me, one that speaks to the history of mathematics and all of its “yellowed textbook” cultural associations with library intellectualism.
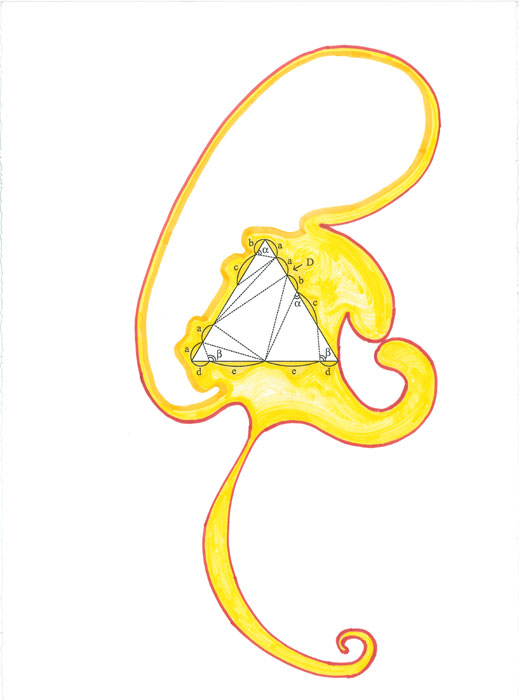
Over the course of my drawing project, I have classified three types of formal elements in mathematics. In the few pages that follow, I will provide images of these isolated formal elements in math, immediately followed by a particular drawing of mine that makes nearly exclusive use of that element. The first set comprises the symbolic, which includes arithmetic and algebra, and probably looks like what most people think of when they imagine “math.” This example is also notable in that it comes from a conference published in 1981, before the advent of LaTeX [66] , a markup language used to produce mathematical documents. So, this particular mathematical phrase on the following page enjoys a historical quality, lent by its being typewritten.
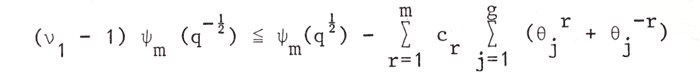
The second type of formal element in math, seen below, is the geometric.
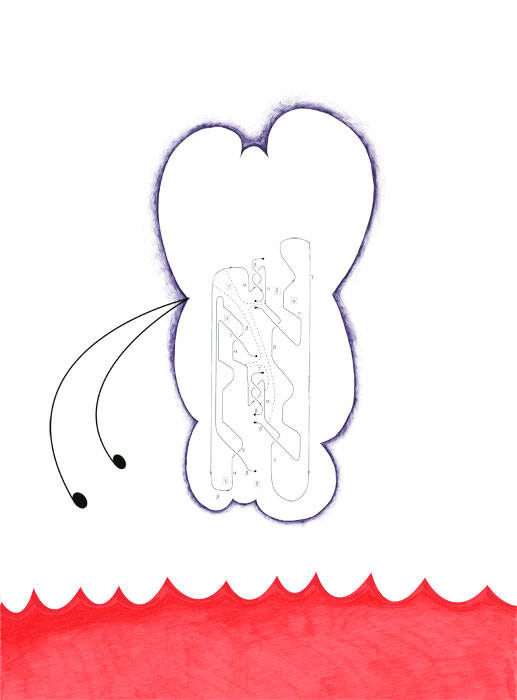
The third type is the diagrammatic. At first glance, or even after a long inspection, a diagrammatic element might appear quite similar to a geometric element. The difference comes from its place within mathematical logic: a diagrammatic element functions representationally, and is more like a symbol, whereas a geometric element functions more as a thing-unto-itself – something that is in itself an end-product, and can be represented with symbols. The example of diagrammatic notation on the next page comes from a book on diagrammatic morphisms, and was described to me by Dr. Dan Christensen of the University of Western Ontario Department of Mathematics as “a tube wrapped around a knot.”
These three elements – the symbolic, the geometric, and the diagrammatic – constitute one strategy within my drawing practice: copying math, and arranging formal elements; essentially, I am painting, drawing, or sculpting with math. The other approach is to do math – in my case, I am restricted to arithmetic, simple algebra, and first-year calculus – and then present this as art-object. I term this approach the organic, which is exemplified on the following page.
It can be noted that this last type – the organic – has the potential to be a wider category, and in fact one that might itself contain geometric, algebraic, and diagrammatic elements. In that sense “the organic” is not so much a formal categorization as it is an analysis of process. But with that in mind, “organically” producing math, or in this case a math-drawing, yields a particular formalism that might be impossible to produce when copying math out of books. The most important of my drawings that follows an organic process of creation that yields organic formal elements has been titled “the power rule.”
For the creation of “the power rule,” I re-learned some of the calculus that had almost totally escaped my memory and took derivatives on drawing paper (using the power rule of differentiation). The concept and process surrounding "the power rule" are so vital, from my perspective, that it becomes difficult for me to analyze the drawing objectively and formally, and ascertain whether or not it is working as a visual object. Even if it were not working, this drawing is immensely important to me and to my project of “the look of math.”
Perhaps, in the case of these “organic” math drawings, the awareness that the results are destined to be “art objects” colors the process of doing math, such that the math done in these drawings has a different look than math done on a homework assignment or test. The visual structure of my notes and tests in math class became important to me, even so many years ago, before the idea for “math as art” specifically and overtly occurred to me courtesy of Dieter Roth, my day planners, and my own hint of an academic background in math.
The division of aesthetic formalism to be found in mathematics [67] into the symbolic, the geometric, the diagrammatic, and the organic is, like any system of categorization of pre-existing objects, imperfect. This was demonstrated to me as I tried out collage in my math drawings, and was arranging cut-out bits of photocopied math into piles according to these categories. Most of the cut-outs obviously fit into one or another formal category, but occasionally I encountered some ambiguity, as in the case of certain paper cut-outs that were diagrammatic but looked geometric. I knew they were diagrammatic because I had read about them, and knew their source. Perhaps if I had not, I would not have thought twice about putting these bits into the “geometric” pile. My project is about “the visuality of math” – the way the written markings of math look, apart from their function as a logical system. Translating this into a kind of ethic, does this not mean that I should make a decision based purely on how the shape in front of me looks? In a sense this scenario feels like a test case to gauge whether or not I am in good faith regarding my hypothesis, which presumes that some-thing’s inner and outer natures are separable. When I take a diagrammatic object that looks geometric and put it in the geometric pile, I tend to feel uneasy, because in a mathematical way I think “No, this is wrong,” while in an aesthetic or artistic way I am forced to concede “This is right.”
In addition to my math drawings, my practice also continues to involve materials from the digital domain, in which I was trained as an undergraduate. Sound art is one manifestation that may be conceptually digressive regarding this thesis because it appears to be an example of “math-in-art” as opposed to “math-as-art.” In other words, the sound art that I do is inherently mathematical, and inherently physics-based; it involves the creation of specific pitches that are numerically related to one other, and using this set of “new notes” – notes that do not exist in Western music – to create roughly three-minute compositions of similar form (pitches composed of pure sine waves intersect and create intervals and even occasionally chords, while a guitar that has had its strings re-tuned to match the sine waves is played along).
As an example of my sound work, one composition is based on a series of known and often-used mathematical constants, such as pi (roughly 3.142) [68] and e (roughly 2.718). In order to generate an interval, or a pairing of notes, based on this constant, one assigns one note the value of “1” and then the other note the value of the constant (say, 3.142). Then, say the first note is pitched at 100 Hz; using a simple proportion equation, one then figures the second note to be 314.2 Hz in order to match that “1 to pi” ratio (actually, as you can see in the chart on the next page, my base was 82.407 Hz, so-chosen because it is the frequency of the low “E” string used in standard guitar tuning). This process is repeated for all six notes, using one note as a “base,” and choosing such mathematical constants as to make re-tuning the guitar strings to match them involve as little deviation from a given string’s intended tension as possible.
| Guitar string | Constant | Constant value | Multiplied by | Frequency in Hz |
| E | base | 1 | 82.407 | 82.407 |
| A | Plastic Constant | 1.325 | 82.407 | 109.189 |
| D | Golden Ratio | 1.618 | 82.407 | 133.334 |
| G | e | 2.718 | 82.407 | 223.982 |
| B | pi | 3.142 | 82.407 | 258.923 |
| e | Lévy's Constant | 3.276 | 82.407 | 269.965 |
The chart above shows the 6 guitar strings (and 6 pitches used), as well as the name of the mathematical constant with which a given string is associated, the value of the “base” by which that constant must be multiplied in order to get a proper frequency for the note, and then the frequency of that note and/or string. This chart demonstrates why this project is not just mathematical but ethnomathematical, and why it is not concerned only with math-in-art but with math-as-art. Simply, it is because the intervals are being chosen based on numbers that are often used in the discipline of math, like the Golden Ratio, Levy’s Constant, and the Plastic Constant. In using these constants to generate my pitches, I am looking directly at mathematics, and not just using it to namelessly generate pitch; in this case, math is an actor in the foreground, and not just the background.
Animation is an obvious synthesis of drawing and sound, and I have come to see it as a culmination and resolution of my art practice, as it has developed in this Master of Fine Arts program.
My undergraduate studies were branded as having an “Imaging and Digital Arts” focus, and all of my work there was classified as “media art”: video or sound projects, produced with some kind of digital device and then exhibited on some kind of digital device. After continuing with this approach in graduate school for a brief period, I discovered that I wanted some material experience – drawing, sculpture, print, etc; something less constrained into a single subculture of contemporary fine art. Later, after several months of this experimentation, I returned to media art (specifically, to soundtracked animation), but did so informed by a surrealistic Kandinsky-Twombly-Miro aesthetic that was not so present in my undergraduate or pre-graduate school work, which tended to look like a synthesis of comic book illustration, graphic design, and Photoshop collage. So, in a sense, the results of my material experimentation served as “concept art” for videos that were, after participation in the discourses within my graduate program, more able to break out of the cultural constraints of traditional animated drawing (specifically, strict character-based conflict/resolution narrative, which is a fairly narrow way to work if used as an exclusive domain).
On the following page are two stills from a short, animated, soundtracked video that uses some of the visual elements of math I isolated in earlier work (diagrammatic, algebraic, geometric, and organic), and which also uses sound to bring a vitality to the mathematical visuality that was less immediate in the drawings. In a sense, my animations are what my drawings want to be, and also what they cannot be.
I stress ethnomathematics over mathematics in order to emphasize that my focus is on math as a cultural relic, like sets of dinosaur bones that indicate some past life. Not only is my artwork not concerned with mathematical content, as it might be used to build a set of interlocking shapes, but it is also important to remember that my artwork is not “about math” in the sense that it demonstrates some quality of mathematics itself, such as using only a prime number of colors or even trying to formally interpret and express some universal quality of math. It is only “about math” in the sense that it showcases the visual relic of math: the lines, marks and symbols that someone doing math puts down on a paper, chalkboard, LaTeX editor, etc. It is the pure visuality of these markings-on-paper with which I am concerned, as well as the relationship they have with the artist, and later, the observer. This relationship is built out of things that exist in the observer’s mind-brain that interact with mathematical symbols, and create new phenomenological objects.
Pure mathematics is like much contemporary “gallery art” in that both are immediately impractical. Both can theoretically be monetized after some time and in some way, but as they are born, neither a proof in category theory nor a nailed-together sculpture made of construction debris can work to achieve any other ends than existing, or perhaps providing a site for discourse.
It might seem that I have written a lot about math, and not very much about art. In fact, that is the nature of the territory in which I am working. Art has become, since the early 20th century and with its first seeds of conceptualism, a category without apparent boundaries. In one of my studio critiques I mentioned that one of the things I liked best about contemporary art as a discipline was this limitlessness: one could, I said, tack up your completed tax forms to a gallery wall and be taken just as seriously as an oil painter or ceramicist. “It’s been done,” someone responded, which got a laugh. The point is that I do not need to talk about art, per se, because talking about art per se has become somewhat redundant in view of our Postmodern de-categorization of styles, media, concepts, and forms.
So, it seems that in post-Postmodernism [69] , I no longer need to justify anything to a committee and explain why it should bear the gilded moniker “art.” No one has, really, since 1917 [70] . So, math-as-art is not revolutionary. Nothing can be revolutionary in art anymore, in fact, and the potential of art to be a research discipline cannot exist in some sense. The word “revolutionary” itself inplies a historical and linear continuity, one that has been halted. The Duchampian revolution in art was disruptive in a similar way that Gödel’s Incompleteness Theorem was disruptive in mathematics (and in the way trans-historical, trans-linear, trans-evolutionary Postmodernism has been to any intellectual discipline): as the latter demonstrated the un-provability of the axioms within a given logical system using only the tools of that logical system, the former similarly posed an axiomatic challenge to art by asking the question “What is it, really?”
I have heard it argued that if indeed the term “art” is so all encompassing, fuzzy-edged, and broad, it in fact loses meaning. I do not disagree, and that is part of the reason I find it mostly unnecessary to talk about “art,” or those creative endeavors that have been termed “art”. This is not an essay in art history, exploring what might be worthy of the label. In order for something to be art now, all that needs to happen is for people to pay attention to that thing – it needs to somehow get pulled out of “the everyday [71] ,” and be reflected upon with a particular awareness, perhaps a meditative one, such as we might find in Zen, in prayer, and perhaps in doing math.
One could take any sort of mental object – chemistry, ladybugs, roll-top desks, racism, etc – and say “this object has never been specifically or importantly isolated as art-per-se.” Duchamp’s Fountain was a statement of the universality of this principle. In a way, writing a thesis on some special case of “anything can be art” might seem unnecessary. Maybe the title of this essay could take the form of “The Look of X,” where X is something, some mental object, some noun, preferably an intellectual discipline or activity like math: The Look of Medicine. The Look of Carpentry. The Look of Sex. Etc [72] . Why, particularly, is my focus on the visual culture of mathematics, and why is singling out anything in post-postmodern modernity and saying “It is notable that this thing can be art if you frame it thusly” still an interesting thing to do? Has it not been done, back in 1917, by Duchamp, with his “R. Mutt” urinal?
The answer and admission, in part, is that it is not interesting. The sort of trans-historicity and trans-linearity that Duchamp opened up was destructive, and an early manifestation of the postmodern impulse or instinct. The evolution of art, in some sense, stopped in 1917; after someone says “Anything can be art,” and people actually listen, the term “art” is no good anymore. Perhaps the real realization is that the term was no good to begin with; unlike math, which is 5000 years old, “art” is only a few hundred. [73] Before then, people who drew, painted, or sculpted did so in a larger cultural context; “art for art’s sake” was a conceptual seed that grew into something that has ultimately become self-destructive. This is what some theorists are alluding to when they refer to the avant-garde as a “failed project.” [74]
So, to say “This thing can be art” is not a novel or interesting concept in and of itself – at least not anymore. What is interesting (I think), is when we start looking at the things themselves and examining the particularities that emerge from their being re-contextualized as “art,” or perhaps as a material in culture we had not encountered in such a way before. So, what if we really were to look at The Look of Carpentry? It might involve displaying some hand tools and nailed-together planks of wood, which is similar to some exhibits I have seen. Yes, anything can be art – this is old news, and pointing it out makes me sound as though I must have slept through art history.
Clearly, I would hope that the focus of this paper has not been a Duchampian musing of “But what is art, really?,” but instead, that it is seen as a close examination of what happens, culturally and visually, when the look of math – a page of done-mathematics – is proverbially tacked up on the gallery wall, and then split into signifier and referent. Tacking the math up in the first place is not that interesting or brilliant or revolutionary; “anything can be art” is not a concept that needs reiteration in the year 2011, and I hope I have not reiterated it too much. Although “math-as-art” implies a novelty of making math into art, my intellectual focus has always been Saussurean – math structured as sign and object, as signifier and referent, and then the beginnings of an exploration of what happens when that structure is pulled apart.
In a sense, my arguments are more about what can be taken away from math than what can be added to art. Art has already been consumed by postmodernism and is therefore in a fractured, trans-historical place that blocks research of its continued linear evolution. But math has not been similarly infected (except arguably by Gödel and his Incompleteness Theorem [75] , which does not generalize to all math), which leaves it open for the central thrust of my explorations: that you can take away the utility of math and be left with some referent-less symbology, which is then ripe for re-assignment.
In closing this discussion, I need to more directly navigate the minefield I entered: why (the visuality of ethno)math? Why not, as I somewhat facetiously suggested, The Look of Carpentry? Because math has special qualities. Math has intellectual clout, it is respected, and it is a symbol of the cult of intelligence that flourishes in so many sectors of society, from the white-collar workplace to academia to internet communities. There is a robustness to mathematics, a strength, and “not only truth, but supreme beauty – a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of paintings or music, yet sublimely pure and capable of a stern perfection such as only the greatest art can show.” [76]
Math intimidates many people [77] , and without a rigorous sociological study I am willing to bet that a disproportionate number of those people are artists. This harkens to my discussion of the humanities-science split in intellectual culture, and furthermore, to the fact that science has been artificially elevated over the humanities in part by the interplay of capitalism, militarism, and nationalism. But I am inclined to think this split is not entirely cultural, however politically incorrect it might be to allude to absolutes or biological causation in human behavior. There exist some polymaths [78] who can do both math and art equally well, but most people are better at one or the other. So, because math constitutes particularly foreign, perhaps particularly intimidating territory for artists and art culture, it thereby and therefore constitutes particularly important territory for artists and art culture.
Math is drawing. This is not to imply that because math is bonded to a pencil-and-paper culture that it should automatically enjoy special art status, but only that the historical import of drawing as a discipline is strong enough that something as obviously similar as the art of doing mathematics appropriates some of that historical import, and in doing so can more readily assume a comfortable place in art culture.
Lastly, the most important answer to “What is the importance of what you are doing?” is quite personal; I have a relationship with the discipline of math, which at this point is over 10 years old and is fading fast from my more active neuro-chemical structures. In order to get some of it back, some of that sense of mastery and accomplishment and in fact visual fulfillment I gained when I was doing math so many years ago, I chisel at it now with a new toolbox. I remember the visuality of math feeling compelling, interesting, and important when I took math classes, and I know (and knew, to an extent) that what I was doing was as much “art” as it was math.
I will summarize my main argument, although there are admittedly some (the preceding pages’ worth of) important addendums to consider: if you pay attention to the way math looks when it is written out, you can experience it on this visual level without working with or understanding the logical content; math has a look, which is not the same thing as math’s inner structure. Furthermore, separating the image of some-thing from that thing’s inner essence, structure, or nature allows new structures to seep in to the empty form, and in turn affect both the observation of that form and our understanding of the complexity of human culture.
Notes
of Interest, Elaboration, and Reference [79]
[1] During my undergraduate study of art, I was taught that Marcel Duchamp was a kind of revolutionary, mythical figure – something like the art world’s version of Lance Armstrong in cycling; an end-all and be-all. It was almost as if his importance could not be overstated. I suspect that this is close to true, at least in a contemporary historical context – i.e., we are where we are now in academic, gallery and museum-based art, and continue to exist where we are now, because of Duchamp’s ideas about conceptualism. I say this with some reservations; I’m not all glowing praises for Duchamp and his ideas, because I think they were destructive and nihilistic in the same ways that postmodernism has turned out to be for any and all creative disciplines to which it attaches itself.
That said, I think we’re stuck – especially in academia – in a sort of conceptual soup that Duchamp originally cooked up, and that we can’t swim our way out of (although he himself swam out of it, as I mentioned in the introduction to this paper – he went off to play chess in Argentina instead of continuing with “art”). Ultimately, postmodern conceptualism is stifling, and is probably going to end up hurting art in the long run, in terms of its development and evolution. In fact it has to hurt it, because the effect of the “Duchampian Revolution” was to stop the evolution of art, in a very postmodern way: we have nowhere to go now, since everything has “been done.”
And I don’t think this is a good place to be – it’s turned the discipline of art into something destructively “meta;” we can think now about the discipline of art and about how it’s not going anywhere, while we borrow our vocabularies from 20th century continental philosophers like Derrida, Foucault, Lacan, Lyotard, Bathes, etc, but I’m not sure we can really “study art” anymore, at least not in the same way that students in the music department “study music.” Imagine people training to be plumbers being interrupted in their learning the techniques of plumbing by time spent learning the philosophy of plumbing. Perhaps we should be more like musicians, who devote 4 years of college study to being better musicians. “Total craft immersion” is something that’s being left to the filmmakers and comic book artists, while the skill-sets of artists in academia deteriorate to a point where they only make conceptual art, minimalism, and postmodern smashed-together pastiche, not because they want to, but because they aren’t able to do anything else. In art departments, we study to be conceptual pranksters, but not only that – we study to be the same conceptual prankster, whose pranks were all pulled off almost 100 years ago.
This is not to say that conceptualism and craft are necessarily antithetical – indeed, it is my hope that they are, or can be, complimentary. But it seems that they often amount to an oppositional dichotomy that can readily be misinterpreted as a “one or the other” rhetorical trap, when really the best thing for students to do is to make work that they like and that they’re excited about.
Notably, I begin and end this essay with Duchamp, in spite of or because of these misgivings.
[2] Math is short for mathematics. I use the two words interchangeably and with no analytical determination; “whichever sounds good” comes close to my methodology. Same goes for ethnomath(ematics).
[3] Although Duchamp’s place in “the art world” was virtually eliminated in 1918 by his own hand when he moved to South America, his creative projects continued, whether or not these bore the label “art.” His influence on the intersection of art and intellectual culture continued during the course of his life, and irrespective of his moving in the appropriate cultural circles of the visual arts per se, especially as they were more restrictively defined in the earlier and middle parts of the 20th century.
[4] Alice Goldfarb Marquis. Marcel Duchamp: The Bachelor Stripped Bare : A Biography (Ann Arbour: MFA Publications, 2002)
[5] Pierre Cabanne. Dialogues with Marcel Duchamp (London: Thames and Hudson, 1971)..
[6] “Visuality” refers to the seeable properties of an object, taken apart from other sensory experience. For example, the visuality of a musical concert might include the color of the seats, the hairstyle of the conductor, and the facial expressions on the violinists as they play. The visuality of a film refers only to photons reflecting off the screen and onto the viewer’s retina (and specifically not the soundtrack). The visuality of the entire “film experience” might also include spotting a chewed piece of bubblegum stuck to the theatre floor. Finally, the visuality of math refers to the quality of there being a part of the math that you can see, and that does not necessarily have anything to do with any other properties of the math (such as the functioning of its logical internalities).
[7] The Shroud of Turin is a piece of material said by some to be imprinted with the image of the crucified Christ. So, a “mathematical Shroud of Turin” would imply that the image of the math has been imprinted, but the math itself has rolled the stone away from the tomb, so to speak. Daniel C. Scavone. The Shroud Of Turin: Opposing Viewpoints. (Farmington Hills: Greenhaven Press, 1969).
[8] In his most important work on aesthetics, 19th century philosopher Clive Bell gives us the notion of “significant form,” which he describes as some essential quality in formalism that is responsible, via an individual phenomenology, for the subjective experience of art, as art. The notion certainly borders on the mystical, and is reminiscent of a more-academic definition of “beauty,” although with less of a value-judgment attached. Clive Bell. Art (Charleston: BiblioBazaar, LLC, 2008) , 15-32.
[9] Doris Schattschneider, Maurits Cornelis Escher, Michele Emmer. M.C. Escher's Legacy: A Centennial Celebration (New York: Springer, 2005), 142.
[10] Ibid., 142.
[11] Michael Emmer. The Visual Mind II (Cambridge: MIT Press, 2005), 11.
[12] Saussure, Ferdinand de. Course in General Linguistics (trans. Roy Harris) (London: Duckworth, [1916] 1983). Although the Course was scientifically important in the early and middle parts of the 20th century, other theorists and methodologies eventually supplanted it as a tool in linguistics. "Saussure's views are not held, so far as I know, by modern linguists, only by literary critics, Lacanians, and the occasional philosopher" (Holland, Norman N. (1992) The Critical I, Columbia University Press). Perhaps it is the tendency of the postmodern to cling to outdated science, even as it presents a critique of science.
[13] Ubiratan D'Ambrosio, a Brazillian educator, coined the term in 1977, and admitted that the meaning was never straightforward.
[14] Allen J. Bishop. Second International Handbook of Mathematics Education, Volume 1 (New York: Springer, 2003), 82.
[15] Arthur B. Powell, Marilyn Frankenstein. Ethnomathematics: Challenging Eurocentrism in Mathematics Education (Albany: SUNY Press, 1997), 6.
[16] Helaine Selin, Ubiratan D'Ambrosio. Mathematics Across Cultures: the History of Non-Western Mathematics (New York: Springer, 2001), 18.
[17] Anthropology is the formal, often academic study of human culture and human behavior. So, I find it appropriate to term my flavor of ethnomathematics as an anthropological ethnomathematics; in fact, something like “the anthropology of mathematics” might be even clearer, except there are some connotation to that which might be better avoided; the line between ethnography and anthropology is a fine one (as is the line between anthropology and sociology – or perhaps I should say these are particularly fine lines, as any two intellectual disciplines inevitably enjoy a plane of intersection), with “anthropology” connoting, at least to me, a comparative study of culture across time and geography while ethnography connotes the analysis of a particular culture. So, then, ethnography of mathematics? Sociology of mathematics? I think any of these would work, as long as the central idea of “the study of the culture of mathematics” enjoys focus. And, in fact, differentiating between ethnography, sociology, and anthropology isn’t really a useful practice when it comes to my studio research, since that research is not all that specific or limited in scope; it is artwork, after all, and tends to go where it will go, so to speak.
[18] I want to approach the second possible definition of ethnomathematics that is currently used in contemporary scholarship, only because it is in common use and I want to ensure that my work does not fall under its umbrella. When some writers mention ethnomathematics, they are referring specifically to any mathematical system that is non-Western, and in doing so are committing the same error that an anthropologist might when he talks about “ethnic” practices applying only to uncontacted tribes in New Guinea and the shape of their arrowheads, rather than the more familiar activity of someone in the anthropologist’s home town visiting a convenience store and buying a hot dog.
Used in this way, scholarship can appear to function as a tool that demonstrates power and establishes itself in a high-up place within a political or cultural hierarchy. This is a common phenomenon, in psychology as well as in sociology – part of the appeal of a psychiatric diagnosis is that in making it the subject is turned into a lab rat and thereby made less. The necessary power relationship between experimenter and subject, such as in the case of a biologist establishing controls for his or her experiments on rats or fruit flies, presents an inherent danger in some areas of sociology or anthropology. In fact, the phrase “establishing controls for experimentation” is a good clue as to the inherent power relationships present in science and extant between experimenter and subject. When the subject is an aspect of human culture (as in the case of sociology or anthropology) or the human mind (as in the case of psychology) then the situation becomes political.
Although any cultural practice of mathematics can fall under “ethnomathematics,” when Western scholars use the term they are often talking about non-Western math. Furthermore, by using the term “ethnomathematics” Western anthropologists are in danger of devaluing the mathematical systems of other cultures by describing them as being primitive and not “real” mathematics, even though a given non-Western system might work just as effectively at solving problems within its containing culture as the math within Western culture works at solving its problems (i.e., building jet fighters or establishing controls for physical experiments).
It has been remarked, often within a Marxist framework or discourse, that “all is politics,” and by implication that trying to shut out or suppress the inherent political considerations that inevitably arise from a variety of discussions amounts to “intellectual fascism.” Recognizing this, and furthermore agreeing with the basic principle (that “politics,” defined as human power relationships, is inevitable, and purposefully ignoring it functions as a tool of de-politicization, a process which disenfranchises the population and keeps power in the hands of a ruling elite), my resistance to this politicized definition of ethnomathematics is born of the fact that it could turn my project in a direction away from aesthetics. So, I use the term “ethnomath” as a way of talking about mathematical practices apart from internal structures, and most crucially, as a thing that will give rise to a visual culture which can be approached as art by an observer. Ultimately, the problem I am pointing to here can be boiled down to the fact that “ethnomathematics” could be used both to describe something that, in postmodern language, could be called neocolonialism, and also to describe the culture of math.
There is an ethnicity and an ethnology inherent in conventional notions of Western mathematics: it has been described as “white male mathematics,” and some people, especially those in math and in the sciences, think the very notion of the term is nonsense, or even offensive, dishonest, or harmful, reasoning from the standpoint of “1 + 1 = 2, regardless of what gender and race you self-report as.” Arguing against the existence of white male mathematics is easy: because Western mathematics works to achieve goals like building the aforementioned jet fighters or establishing the aforementioned controls of physical experimentation, Western mathematics itself appears to argue that it is the only way to do mathematics – i.e., it works. However, it is important to remember that the goals of Western applied mathematics are not the same as the goals associated with systems like Vedic math in India, or Yoruba mathematics in Africa – these systems also work to solve culture-specific problems, and in that sense they are a correct system for that given culture (whereas Western mathematics would not be, in those cases).
Arguing that there might be something of value to be gained from to the term “white male mathematics” is not difficult either. As I noted above, Western math does not have to constitute the only kind of math, because the applied math of other cultures are designed to solve different problems than the ones Western math solves. Furthermore, those doing Western math over the centuries from Plato to Leibniz to Poincaré to Perelman have been white and male (although not necessarily Western, as the last and many other examples demonstrate). This is in itself an ethnomathematical argument, or perhaps even a realist argument: because white males were (and often still are) the ones doing the math, this supersedes an argument that the math somehow transcends human subjectivity. Simply put, Western mathematics is obviously equated with “white male mathematics,” because white males constituted, up until perhaps very recently, the overwhelming majority of the ones doing the mathematics.
[19] Mark Balageur. Platonism and Anti-Platonism in Mathematics (New York: Oxford University Press US, 2001).
[20] Kulturkampf – “Culture War”. Origins are 19th century German church vs. state struggles.
[21] National Science Foundation Authorization Act of 2007: Report. DIANE Publishing.
[22] The degree to which “right-brained” and “left-brained” are either real, physical divisions of labor performed by the brain, or cultural metaphors for splitting up our realities with that same “Derridean Binary” format I keep mentioning, which probably is born of our bilateral symmetry (two eyes, two arms, two legs, etc), is not agreed-upon. However, directions in brain science seem to imply that things are not as “clear cut,” in terms of particular areas of the brain being tasked exclusively with particular cognitive assignments, as we thought 50 or even 20 years ago. So, it is with this in mind that I use the terms “right brained” and “left-brained”. It is not my intent to promote a reactionary, reductionist world-view – one that excessively maps A to B in what might be called an overly-mathematical approach to metaphysics – but only to (or perhaps mostly to) employ a cultural metaphor, which I am explaining as well as helping to create. In other words, the subject of my studies is in part about the division of intellectual reality into “left brained” and “right brained” enterprises, and why this division takes place; it’s not really about confirming the existence of something carved in stone (or perhaps grey matter).
[23] Quantum gravity attempts to reconcile quantum mechanics with general relativity.
[24] Alan D. Sokal. The Sokal Hoax: The Sham That Shook the Academy. (Lincoln: U. of Nebraska Press, 2000).
[25] John McCumber. Philosophy and Freedom: Derrida, Rorty, Habermas, Foucault (Bloomington: Indiana University Press, 2000), 44.
[26] The “irrational rationality of capitalism” is Michel Foucault’s phrase, which is often used in a slightly wider context than intended to associate sci-tech disciplines with the financial interests of the ruling class. In the essay from which this phrase is taken, Foucault used it specifically in reference to Weberian economics. In capitalist economic theory, concepts like “perfect competition” are used to illustrate the mechanical, dispassionate workings of the free market, as though it were reducible to a perfectly predictable or controllable machine. While this is certainly not the case, as has been demonstrated by events like stock market crashes, it is notable that Marxist economics is also sometimes described as a science, showing us that the borrowing of rationality or logic to justify some political ends is not an exclusive sin of free-market fascism. Michel Foucault, Graham Burchell, Colin Gordon, Peter Miller (Ph. D.). The Foucault Effect: Studies In Governmentality : With Two Lectures By And An Interview With Michel Foucault (Chicago: U. of Chicago Press, 1991), 78.
[27] Einstein, of course, was a Swiss patent clerk who did theoretical physics in his spare time.
[28] Perleman was similar. He lived with his mother in near obscurity in Russia, and refused the Fields medal on the grounds that he “didn’t need it.”
[29] “Anti-realism” is the proposition that there is no objective reality, a template or set of ideas against which actuality can be judged. Nietzsche wrote extensively on anti-realism, and was one of its most famous proponents. Plato, on the other hand, was a realist, notably in his philosophy of mathematics. Conversely, a realist position asserts the existence of such a template, and often carries with this assertion connotations of extant divinity, since nothing else could produce an ideal against which all naturally-occurring phenomena might be judged and measured.
[30] T. Koetsier, Luc Bergmans. Mathematics and the Divine: a Historical Study, Volume 2004 (San Diego: Elesvier, 2005), 79.
[31] Kenneth Sylvan Guthrie, David R. Fideler. The Pythagorean Sourcebook and Library: an Anthology of Ancient Writings (Grand Rapids: Phanes Press, 1987), 52.
[32] David Oliver. The Shaggy Steed of Physics: Mathematical Beauty in the Physical World (New York: Springer, 2004), 18.
[33] Steve Awodey. Category Theory (Oxford: Oxford University Press, 2006),1.
[34] James Roy Newman. The World of Mathematics, Volume 3 (New York: Courier Dover Publications, 2000),1871.
[35] Willem Kuyk. Complementarity in Mathematics: A First Introduction to the Foundations of Mathematics and Its History (New York: Springer, 1977), 71.
[36] David E. Radford, Fernando José Oliveira Souza, David N. Yetter. Diagrammatic Morphisms and Applications: AMS Special Session on Diagrammatic Morphisms in Algebra, Category Theory, and Topology, October 21-22, 2000, San Francisco State University, San Francisco, California, Volume 2000 (Providence: AMS Bookstore, 2003), 1.
[37] Giandomenico Sica. What Is Category Theory? Volume 3 of Advanced Studies In Mathematics And Logic (Milan: Polimetrica s.a.s., 2006), 222.
[38] David E. Radford, Fernando José Oliveira Souza, David N. Yetter. Diagrammatic Morphisms and Applications: AMS Special Session on Diagrammatic Morphisms in Algebra, Category Theory, and Topology, October 21-22, 2000, San Francisco State University, San Francisco, California, Volume 2000 (Providence: AMS Bookstore, 2003), vii.
[39] Daniel Perrin. Algebraic Geometry: an Introduction (New York: Springer, 2008), 20.
[40] H. E. Huntley. The Divine Proportion: A Study In Mathematical Beauty (Mineola: Courier Dover Publications, 1970).
[41] Jerry P. King. The Art of Math (New York: Plenum Press, 1992), 284.
[42] Wikipedia, perhaps now close to universally known as a free-content, publically-editable encyclopedia, has been cited to illustrate that when “mathematical beauty” is popularly defined or described, it is often accompanied by some graphic illustration to emphasize the point of “beauty,” even though “mathematical beauty” does not necessarily have a direct relationship with visuality. Wikipedia contributors, “Mathematical Beauty,” Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Mathematical_beauty&oldid=359408327. Citing or using Wikipedia has become such a cultural bugbear in academia that I felt I had to justify my actions somehow.
[43] H. E. Huntley. The Divine Proportion: A Study in Mathematical Beauty (Mineola: Courier Dover Publications, 1970), 143.
[44] Paul J. Nahin. Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills (Princeton: Princeton U. Press, 2006), 3.
[45] A “shear injury” is kind of brain injury that comes about when a sharply rotated brain-case causes the brain to twist against itself, severing neurons as they are rapidly over-stretched. Shear injuries are common in motor pedestrian incidents (people getting hit by cars).
[46] When someone talks about “my brain” or “my body,” an obvious metaphysical issue is raised: what or who is the “me” in “my brain” or “my body”? A soul, maybe? A pre-scientific concept, I think (as might even be “mind”). So is this a relic of a language that has not kept pace with the evolution of science? Or perhaps it’s something deeper: a notion of some universal consciousness? Does it have spiritual implications?
[47] Centre for Educational Research and Innovation, Organisation for Economic Co-operation and Development. Understanding The Brain: The Birth Of A Learning Science, Volume 2. (OECD Publishing, 2007), 114.
[48] I say “tautological” because God is, in some sense, the only thing that can truly be perfect, and true perfection is a quality that can only exist in God.
[49] William James set out his definition of a mystical experience to be that which is couched in individual experience. http://plato.stanford.edu/entries/mysticism/
[51] People working in science and technology frequently make use of the phrase “trivial” or “non-trivial” to describe something that does not (or does) affect a given field of experiment or production. Recently, other people have started to use the word to sound smart – it has crept into casual conversation. See: note 47, “hand-wavy.”
[52] In undergraduate math programs, “analysis” (of complex and/or real numbers) is usually the last category of courses a student needs to take for degree completion. The first courses in calculus, for which courses in algebra are a preparation, are themselves a preparation and introduction to Mathematical Analysis. Analysis itself is loosely defined as a “deep” study of calculus, where the fundamental principles and theorems of measurement of dynamic quantities are solidified. Jonathan Lewin. An Interactive Introduction to Mathematical Analysis (Cambridge: Cambridge U. Press, 2003), 5.
[53] Frank Morgan. Calculus Lite (Wellesley: A.K. Peters, 1995), 10. Along with providing me with a list of differentiation rules, this was the textbook I used to review my calculus skills, and with which I was able to produce an organic drawing developed from doing math (as opposed to copying math). Hopefully I’m able to do more of these “drawings” formally developed from the visual artifacts of math, partly because they would support my thesis better, and partly because they are more vital, more alive, and more original than an abstract composition of subconsciously-derived shapes and forms, which is then augmented with a few lines of algebra.
[54] Sometimes two given objects will satisfy a given definition; in these cases, they are referred to as being “isomorphic” with respect to that given definition. For instance, the number 1 satisfies the definition of "a square root of 1", since the square of 1 is 1. But in fact there is another number that satisfies the same definition, namely -1, since -1 times -1 is 1. Thus, 1 and -1 are distinct objects that are isomorphic with respect to the definition “the square root of 1.” This illustrates how the delineation between objects can sometimes be blurred. Email conversation with Dr. Michael Misamore. London Ontario and Kingston Ontario, August 4th, 2010.
[55] Roger Penrose, born in 1931, was a British mathematical physicist who created string diagrams (which bear his name) in order to better describe the causal relationships between different points in space and time.
[56] David E. Radford, Fernando José Oliveira Souza, David N. Yetter. Diagrammatic Morphisms and Applications: AMS Special Session on Diagrammatic Morphisms in Algebra, Category Theory, and Topology, October 21-22, 2000, San Francisco State University, San Francisco, California, Volume 2000 (Providence: AMS Bookstore, 2003), 10.
[57] Ibid, 3.
[58] “Handy-wavy” is a term usually restricted to use by mathematicians and scientists, but is one that I find useful. It usually characterizes an imprecise and un-rigorous explanation of something, such that someone attempting it would tend to wave his hands around a lot. It can also refer to concepts themselves, which might be impossible to convey, describe, or define in a precise way. Its usage in an MFA thesis is a bit ironic, considering how much literal hand-waving some artists do when they talk about their work. Unlike “non-trivial” (see: note 64), “hand-wavy” has not, in my observation, (yet?) made its way into a cultural context larger than science, math, and technology, but I think this larger cultural context is ripe for the assimilation.
[59] Strictly defined, intelligence might be something like G, or “general intelligence,” a value that closely tracks a given IQ score. But often intelligence is defined in terms of other mental abilities. However, according to the strict lexicon of a psychometrician, “intelligence” is mostly the ability to recognize patterns and solve problems.
[60] This, I believe, was one of Derrida’s points: that the sort of primitive, dualistic world-view that permeates Western culture is harmful to intellectual, personal, and spiritual growth. In other words, he didn’t just point out the existence of the binary structure with one of its components politically elevated above the other, but went on to say “this is not a good way to go about the machinations of reality.” Without reading (and understanding) a lot of Derrida, it’s difficult to know just how his concept of the binary structure in the way we perceive and subdivide reality into language categories differs from dualism, which has been criticized by enlightened Westerners like Nietzsche (in Beyond Good and Evil).
[61] Duchamp invented “retinal art” as a derisive term to describe art that was conceptually barren.
[62] Duchamp, M., Notes, Champs Flammarion- Center D'art Et De Culture Georges Pompidou, Paris, 1999.
[63] The question of competence is a repeatedly arising concern, although not one that is rigorously pertinent to the main idea of this thesis. Instead of leaving out the subject of my and my audience’s qualifications to present and receive mathematics, I will discuss it here. The issue presents itself in the form of two questions.
First of all, am I qualified to work with math? Do I have some kind of math background? Do I understand what I am putting down? To some extent, I will say “yes.” I probably have more background in math than most people, but this background amounts to nothing beyond a year of calculus, which is not uncommon. “Am I qualified?” is an interesting question to ask considering the context, because this project is largely about taking the math away from math; it is about the way people react to these remaining marks on paper, and also simply what these marks look like. Perhaps I should avoid saying, "simply what they look like", because it is impossible for something as clearly semiotic as math not to have any meaning attached to it. But whether or not I understand the math's original, logical functioning is mostly a moot question. I say “mostly” because in a few of my drawings, the formal elements are actually composed of "done mathematics". One of my favorites, for personal as well as project-related reasons, is a drawing in preparation for which I was able to do a self-study refresher course on my 10 year-old calculus skills and take a few derivatives on drawing paper.
At one point I thought questions like "Do you understand this?" revealed something about the social location of math, which is something I write about. I mean this in the sense of reading this between the lines of the question: “Do you, an artist, understand this great and difficult thing you're making a spectacle of? Are you good enough to do so?” But now, I have come to think questions on whether or not I understand math are based on the semiotic nature of what I am putting down; if I were to write down Spanish or Korean or French, I might be asked "Do you understand Spanish or Korean or French?", and I do not think such a question would be motivated from any position of suspicion of lack of qualifications; it would simply be a natural reaction to any signifier: what is the signified?
Secondly, “Is the audience qualified to look at my work?” This might be the more interesting of these two sub-questions into which I have divided the question of competence, and a large portion of my work deals with it. To answer, I will say that my re-positioning of mathematical symbols for re-assignment of new meaning is perhaps dependent on my audience not being qualified to look at my artwork. The only thing I ask of my audience is that they have some kind of relationship with math, which I know most people do. However, it is possible that taking the mathematical guts away from the math is something that happens in the process of my executing an art project, and even those people who might understand a lot of the math will replace the mathematical meaning with something else.
[64] This is a huge topic, and one that is of some interest to me – in doing these math drawings, I’ve become tainted by the trappings of abstract painting, which is a large area with its own discourse. How is it possible to write theory on abstract image-making? Does it mean that it is all necessarily relegated to the enormous category of the subconscious, or are there some other possibilities there? I mention “an observer’s feelings on abstract art” in a sort of meta-reflexive way, but I am sure there are more possibilities. One other that occurred to me later on is a sort of self-reflection and turning inward towards a total state of introspection and introversion (which is related to considerations of the subconscious, in a Freudian or non-Freudian sense), as one works on and focuses on these “meaningless” formal elements. The process is sort of like grooming yourself in the mirror.
[65] Ralph, Bill. “Bill Ralph's Art From Mathematics.” http://billralph.com/ (accessed June 1, 2010).
[66] Further reading: Wikibooks Conributors, LaTeX (Printellegra Company, 2008). http://bit.ly/dYg5k8 (redirect to Google Books)
[67] There is such a thing as “mathematical formalism,” which is a position in the philosophy of math holding that mathematical statements are valid only as the consequences of symbolic manipulation. If we divide art up into conceptualism (art of the mind) and formalism (art of the eye), then there are some parallels there, most notably in the lack of “depth” common to both mathematical and artistic formalism. For all intents and purposes mathematical formalism can be regarded as the same thing as mathematical anti-realism, a concept which I have brought up many times in this essay. However, in order to avoid confusion with aesthetic formalism, I use the term “anti-realism” or “anti-Platonism.”
[68] If someone is concerned with pure math, one might expect him to expand pi out to somewhere far beyond three decimal places. But, since this particular number (3.142) indicates a pitch, we are stuck in a physical realm where expansion even beyond the first decimal place (or perhaps even the difference between two sequential whole numbers) is insignificant, according to its interpretation by human ear. In short, show me someone who can hear the difference between 314.1 hertz and 314.2 hertz, and I’ll show you a robot. This fact seems to function simultaneously as ethnomathematics and its opposite, whatever that might be called.
[69] Postmodernism is relevant to everything we do, because it has seeped into and affects everything we do. The main concepts of postmodernism are, I think, alluded to in its name: "postmodernism." How can something come after that which is modern? Well, obviously it can't. So, with postmodernism, we've broken the linearity of historical evolution, and all forms, all styles, all end-states are simultaneously occurring. In a postmodern world view, you can no longer say "Here is x, and x maps directly to y", because just what x and y are is not clearly defined, much less the relationship of x to y.
[70] The date of Duchamp’s Fountain, which was an autographed urinal placed in a gallery.
[71] “The everyday” is an important concept in contemporary art, and although it might be presumptuous to try and explain it in a single endnote (especially without a good background in LeFebvre and the Situationists – The Everyday vs. the everyday), I will anyway: the term is contemporarily and ahistorically most useful in relation to the “anything can be art” paradigm shift of the early 20th century and the “total aesthetic environment” that came up around us slowly with the dawn of civilization. In our T.A.E., everything we see around us is designed, embossed, produced or manufactured – essentially, everything is beautiful by Neolithic standards.
Consider the film “The Gods Must Be Crazy,” in which an African tribesman finds a Coke bottle on the ground that had dropped out of an airplane. This is immediately regarded as the most beautiful (and useful) object the tribe has ever seen. But, it is not remarkable to us (although it certainly is, compared to rocks and wood and even the “unfinished” home-stitched clothing of the middle ages) because everything around us looks this way: we live in an age of super-design. So, if everything around us is art and nothing is worth looking at, and then we hear Duchamp et al saying “anything can be art,” the next step is to regard the non-beautiful as art, and to use our powers of perception to transform anything into art.
If our physical environment has been destroyed by Capitalism and industry, the only choice is to use our powers of meditation and draw some arbitrary object – let’s say a urinal – out of the realm of “the everyday,” and turn it into art.
[72] My original title was Ethnomathematics, Mysticism, and Representation: The Phenomenology of Math’s Visual Culture. Really, the focus was “ethnomathematics.” “Representation” got put in because the thesis was and is about visual art (or, specifically, the visuality of math). “Mysticism,” on the other hand, was a little harder to justify and was a relic of some designs I had earlier in my residence in UWO’s MFA program, when I wanted to do art and thesis-work related to “spirituality,” without a good understanding of just how ill-defined that term is. “Phenomenology” is the pet philosophical lapdog of the visual arts, since it refers to a world view built from individual sensory experiences – tailor-made, if you will.
Ultimately, I ended up lifting out a considerable number (5-10) pages on mysticism (my answer to the fuzziness of the term “spirituality” – mysticism has a bit more academic clout, at least, and some library literature behind it), and I feel that my thesis is better for it. That said, I don’t want to imply that mysticism has no place in mathematics, ethnomathematics, or visual art. In fact, it might be a sort of binding glue that holds all of these together. However, the problem with writing about mysticism is that it’s very hard not to have your analyses sound very general. One could take “mysticism” and throw it into just about any text and (perhaps) convincingly argue that it has a necessary, vital place in the thesis. And it might – the nature of mysticism might be that it does have a necessary and vital place in any argument. But this kind of “everything is everything” thought makes for sloppy academics and sloppy prose, and it starts to become detrimental to making sense and sounding sufficiently non-crazy.
My second title was Ethnomathematics and Visual Culture, but I abandoned that because it sounds pompous and abstruse, and “visual culture” has become a tired buzzword. The Look of Math is, I think, refreshing and accurate.
[73] When I say “art is only a few hundred years old,” I mean “art” as in “art for art’s sake” – art that is focused on itself, certainly after the advent of Modernism in the 19th century and perhaps even during and after the Renaissance. Certainly, say, Chinese calligraphy and Egyptian tomb hieroglyphics are thousands of years old, and although it’s impossible to read the minds of those artisans, there exists a historiographical consensus that the focus of these projects was some purpose outside of their creation, in and of itself.
[74] Peter Bürger, Michael Shaw. Theory of the Avant-Garde (Manchester: Manchester U. Press ND, 1984), 57.
[75] I’ve been curious for some time about how Postmodernism might have affected mathematics (or, at least how it might be reflected in mathematics), and Gödel’s Incompleteness Theorem is the best example I can come up with. It is my understanding that the theorem is frequently misquoted and misunderstood, especially by people seeking to draw literary metaphors from it, which is something we see in other areas like chaos theory (“you can’t predict this thing, no matter how hard you try”), the Heisenberg uncertainty principle (“you can’t observe this thing without affecting this thing”), and various interpretations of quantum mechanics (usually something to do with free will vs. determinism). In all of these cases, people “in the humanities” draw from incomplete or just wrong understandings of these scientific ideas, metaphors or philosophical notions that apply to some aspect of reality. And while the lessons in the metaphors might not be wrong, per se, it is still based on a skewed notion of a given scientific idea, which is something that tends to annoy scientists.
The metaphor that one might draw out of Gödel’s Incompleteness Theorem is, basically, that the truths we cling to are ultimately subjective, and cannot be shown to be otherwise inside of the same universe – that we’re locked inside of a small room with arbitrary rules and properties, and that the “universality” of these rules and properties is far from assured. This sounds to me like a very postmodern idea.
[76] Attributed to Bertrand Russel.
[77] “Math anxiety” is a “real” disorder that has been studied, measured, written about, treated, etc. It is, perhaps obviously from its name, a problem that arises when students have an undue fear of mathematics. This widespread intimidation by mathematics is another indicator of math’s social location. Perhaps in 1910, when the tables were turned and the humanities were “elevated” over the sciences (at least according to Bertrand Russel), people had “philosophy anxiety.”
[78] “Polymath” is a word that has nothing per se to do with math, but rather refers to someone like Leonardo Da Vinci, who defies or transcends the usual way in which people seem to be born with mental gifts that focus either on the quantitative or the artistic.
[79] I enjoyed working with my endnotes, and they border on being nontraditional. For instance, the first word in my thesis is "Duchamp", a numbered reference referring to an endnote about Duchamp, which is about 500 words long. A pattern is established, and I use my endnotes as kind of a "free writing zone" where I can talk about and elaborate on topics at any length I want and in a more conversational style, something that might interrupt the flow of the main body of text if the endnotes were folded into it.
Akiyama, Jin; Baskoro, Edy Tri; Kani, Mikio (Eds.). Combinatorial Geometry and Graph Theory. Berlin: Springer, 2005.
Aronson, Elliot; Lindzey, Gardner. Handbook of Social Psychology: Special Fields and Applications. New York: Routledge, 1984.
Atlan, Henri. Enlightenment to Enlightenment: Intercritique of Science and Myth. Albany: State University of New York Press, 1993.
Awodey, Steve. Category Theory. Oxford: Oxford University Press, 2006.
Barrow, John D. Pi in the Sky: Counting, Thinking, and Being. New York: Oxford University Press, 1992.
Barton, Bill. The Language of Mathematics: Telling Mathematical Tales. New York, NY: Springer, 2008.
Bell, Clive. Art. Charleston: BiblioBazaar, LLC, 2008.
Bergmans, Luc; Koetsier, T. Mathematics and the Divine: a Historical Study, Volume 2004. San Diego: Elesvier, 2005.
Bishop, Allen J. Second International Handbook of Mathematics Education, Volume 1. New York: Springer, 2003.
Bray, Francesca. Graphics and Text in the Production of Technical Knowledge in China: the Warp and the Weft. Boston: Brill, 2007.
Browne, Edward Granville. A Year Amongst the Persians: Impressions as to the Life, Character, and Thought of the People of Persia, Received During Twelve Months’ Residence in that Country in the Years 1887-8. London: A. and C. Black, 1893.
Burchell, Graham; Foucault, Michel; Gordon, Colin; Miller, Peter, Ph. D. The Foucault Effect: Studies In Governmentality : With Two Lectures By And An Interview With Michel Foucault. Chicago: U. of Chicago Press, 1991.
Burdick, Bruce Stanley. Mathematical Works Printed in the Americas, 1554-1700. Baltimore: Johns Hopkins University Press, 2009.
Bürger, Peter; Shaw, Michael. Theory of the Avant-Garde. Manchester: Manchester U. Press ND, 1984.
Cabanne, Pierre. Dialogues with Marcel Duchamp. London: Thames and Hudson, 1971.
Cutkosky, Steven Dale. Toroidalization of Dominant Morphisms of 3-folds, Issue 890. Providence: AMS Bookstore, 2007.
D'Ambrosio, Ubiratan; Selin, Helaine. Mathematics Across Cultures: the History of Non-Western Mathematics. New York: Springer, 2001.
Duchamp, Marcel. Notes, Champs Flammarion- center d'art et de culture Georges Pompidou, Paris, 1999.
Emmer, Michael. The Visual Mind II. Cambridge: MIT Press, 2005, 11.
Emmer, Michele; Escher, Maurits Cornelis; Schattschneider, Doris. M.C. Escher's Legacy: A Centennial Celebration. New York: Springer, 2005.
Fideler, David R.; Guthrie, Kenneth Sylvan. The Pythagorean Sourcebook and Library: an Anthology of Ancient Writings. Grand Rapids: Phanes Press, 1987.
Field, Michael J. Symmetry in Chaos: a Search For Pattern in Mathematics, Art, and Nature. Society for industrial & applied Mathematics, 2009.
Frankenstein, Marilyn; Powell, Arthur B. Ethnomathematics: Challenging Eurocentrism in Mathematics Education. Albany: SUNY Press, 1997.
Graham, Loren R. Naming Infinity: a True Story of Religious Mysticism and Mathematical Creativity. Cambridge, Mass.: Belknap Press of Harvard University Press, 1999.
Hoffman, Johan; Johnson, Claes; Logg, Anders. Dreams of Calculus: Perspectives on Mathematics Education. New York: Springer, 2004.
Holroyd, F. C and Wilson, R. J. Geometrical Combinatorics. London: Pitman Publishing, 1984.
Holt, Michael. Mathematics in Art. New York: Van Nostrand Reinhold Co., 1971.
Huntley, H. E. The Divine Proportion: A Study in Mathematical Beauty. Mineola: Courier Dover Publications, 1970.
Ingal, Carol K. Metaphors, Maps, and Mirrors: Moral Education in Middle Schools. Westport: Greenwood Publishing Group, 1997.
Jardine, Dick; Shell-Gellasch, Amy. From Calculus To Computers: Using The Last 200 Years Of Mathematics History In The Classroom. Cambridge: Cambridge U. Press, 2005.
Kaplan, Robert. The Art of the Infinite: the Pleasures of Mathematics. New York: Oxford University Press, 2003.
King, Jerry P. The Art of Mathematics. New York: Plenum Press, 1992.
Kline, Morris. Mathematics in Western Culture. New York: Oxford University Press, 1953.
Kuyk, Willem. Complementarity in Mathematics: A First Introduction to the Foundations of Mathematics and Its History. New York: Springer, 1977.
Lave, Jean. Cognition in Practice: Mind, Mathematics, and Culture in Everyday Life. Cambridge: Cambridge University Press, 1988.
Lewin, Jonathan. An Interactive Introduction to Mathematical Analysis. Cambridge: Cambridge U. Press, 2003.
Lieber, Lillian R. Human Values and Science, Art and Mathematics. New York, Norton, 1961.
Marquis, Alice Goldfarb. Marcel Duchamp: The Bachelor Stripped Bare: A Biography. Ann Arbour: MFA Publications, 2002.
McCumber, John. Philosophy and Freedom: Derrida, Rorty, Habermas, Foucault. Bloomington: Indiana University Press, 2000.
Morgan, Frank. Calculus Lite. Wellesley: A.K. Peters, 1995.
Nahin, Paul J. Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills. Princeton: Princeton U. Press, 2006.
Newman, James Roy. The World of Mathematics, Volume 3. New York: Courier Dover Publications, 2000.
Oliver, David. The Shaggy Steed of Physics: Mathematical Beauty in the Physical World. New York: Springer, 2004.
Pluth, Ed. Signifiers and Acts: Freedom in Lacan's Theory of the Subject. Albany: SUNY Press, 2007.
Preus, Anthony. Essays in Ancient Greek Philosophy: Before Plato. Albany: SUNY Press, 2001.
Purohit, Tani Nibedita, Culture, Cognitive Style, and Mathematics. London, Ontario: Faculty of Graduate Studies, University of Western Ontario, 1993.
Radford, David E.; Souza, Fernando José Oliveira, Yetter, David N. Diagrammatic Morphisms and Applications: AMS Special Session on Diagrammatic Morphisms in Algebra, Category Theory, and Topology, October 21-22, 2000, San Francisco State University, San Francisco, California, Volume 2000. Providence: AMS Bookstore, 2003.
Ralph, Bill. “Bill Ralph's Art From Mathematics.” http://billralph.com/ (accessed June 1, 2010).
Recorde, Robert. The Whetstone of Witte, Whiche Is The Seconde Parte Of Arithmeteke: Containing The Extraction Of Rootes; The Cossike Practise, With The Rule Of Equation; And The Workes Of Surde Nombers. J. Kyngstone, 1557.
Restivo, Sal P. The Social Relations of Physics, Mysticism, and Mathematics: Studies in Social Structure, Interests, and Ideas. Boston: Kluwer, 1983.
Rothman, Tony. Doubt and Certainty: the Celebrated Academy: Debates on Science, Mysticism, Reality, in General on the Knowable and Unknowable, with Particular Forays into Such Esoteric Matters as the Mind Fluid, the Behavior of the Stock Market, and the Disposition of a Quantum Mechanical Sphinx, to Name a Few. Reading, Mass.: Perseus Books, 1998.
Russell, Bertrand. Mysticism and Logic, and Other Essays. London: Penguin Books, [1953]
Saussure, Ferdinand de. Course in General Linguistics (trans. Roy Harris). London: Duckworth, [1916] 1983.
Scavone, Daniel C. The Shroud Of Turin: Opposing Viewpoints. Farmington Hills: Greenhaven Press, 1969.
Scully, Robert J. The Demon and the Quantum: from the Pythagorean Mystics to Maxwell's Demon and Quantum Mystery. Weinheim: Wiley-VCH, 2007.
Segerstråle, Ullica; Olofsdotter, Christina. Beyond The Science Wars: The Missing Discourse About Science And Society. Albany: SUNY Press, 2000.
Sica, Giandomenico. What Is Category Theory? Volume 3 of Advanced Studies In Mathematics And Logic. Milan: Polimetrica s.a.s., 2006.
Smith, David Eugene. History of Mathematics. New York: Dover Publications, 1958.
Smith, Margaret. An Introduction to Mysticism. London: Sheldon Press, 1977.
Stanford Encyclopedia of Philosophy. “Mysticism.” http://plato.stanford.edu/entries/mysticism/ (accessed May 14th, 2010).
Turner, Frederick. Beauty: the Value of Values. Charlottesville: University Press of Virginia, 1991.
Tweed Museum of Art. Contemporary Art and the Mathematical Instinct. Duluth, Minnesota: Tweed Museum of Art, 2004.
Verran, Helen. Science and an African Logic. Chicago: U of Chicago Press, 2001.
Warshaw, Margaret. Mathematics Education Within the Postmodern. Greenwich, Conn.: information age Pub., 2004.
Watt, Thomas Meikle. The Intuition of God: An Introduction to the Philosophy of Mysticism ; the Hastie Memorial Lectures Delivered at Glasgow University. London: W. Blackwood & Sons, Ltd., 1929.
Zaslavsky, Claudia. Africa Counts; Number and Pattern in African Culture. Boston: Prindle, Weber & Schmidt, 1973.